MatCalc version: 5.43 - …
Author: E. Kozeschnik
Created: 2011-09-20
Revisions:

This paper describes how the precipitate shape is implemented into the MatCalc precipitation framework.

None

The original MatCalc precipitation kinetics model for growth has been developed under the assumption of spherical precipitates.¹⁾ In later studies, the treatment has been extended to account for needle and plate-shaped precipitates, too.

The implementation of non-spherical precipitate shape is realized in the form of a shape factor $h$, which is described below. Non-spherical shape has major influence on the following features of precipitation kinetics simulations:

• Nucleation: The effective interfacial area is increased by non-sphericality, simultaneously, the specific interfacial energy is reduced due to modified bond interactions across the precipitate.
• Growth: The diffusion fields surrounding non-spherical precipitates are distorted. As a consequence, plate-like precipitates grow faster compared to needle-shaped.
• Strengthening: The mean distance between non-spherical precipitates on the dislocation glide plane is generally smaller than the distance between spherical ones. This feature is reflected in the lower value of the inter-particle spacing $\lambda$. Precipitation strengthening is more pronounced in systems with non-spherical precipitates.

Note that the variables D_MEAN$phase, HEQ_MEAN$phase and DEQ_MEAN$phase can be utilized to evaluate the geometric properties of the non-spherical precipitates. This is elaborated later.

A simple geometrical object that can be used to represent needle-shaped as well as plate-shaped precipitates with a simple shape factor $h$ is the cylinder defined by a height $H$ and a diameter $D$. This object is shown in the figure below.

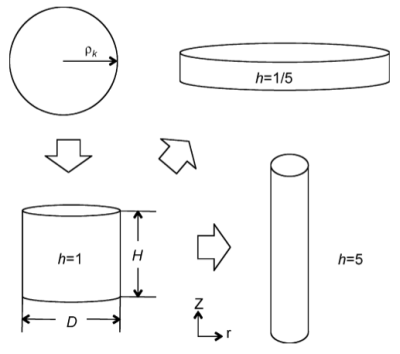Figure 1: Definition of shape factor

With this assumption, a shape factor $h$ can be defined as

\[h=\frac{H}{D}\]

with $h=1$ representing a symmetric cylinder, and $h>1$ representing needle-shaped precipitates, and $h<1$ plates.

With this definition, the influence of non-spherical shape has been investigated in several aspects. These are discussed below.

This feature is not yet implemented in MatCalc. First versions of theory for non-spherical nuclei have been developed, though, and will be implemented and published in the near future. Hopefully.

In the original SFFK model for precipitate growth, the precipitates are surrounded by radial (or spherical) diffusion fields. This assumption has provided a very convenient means for formulation of the evolution equations. In the case of non-spherical precipitates, the diffusion fields are no longer spherical, but they are distorted by the precipitate shape. In a numerical study²⁾ using the Finite Element Method, the growth rates of non-spherical precipitates have been investigated in relation to the growth rate of the symmetrical cylinder.

In a first step, the original SFFK model has been reformulated to account for the influence of non-sphericalicity in the form of four parameters, $S_k$, $K_k$, $I_k$ and $O_k$. The Gibbs energy $G$ of the precipitation system then reads

\[ G=\sum^n_{i=1}N_{0i}\mu_{0i}+\sum^m_{k=1}\frac{4\pi\rho^3_k}{3}\left(\lambda_k+\sum^n_{i=1}c_{ki}\mu_{ki} \right) +\sum^m_{k=1}4\pi S_k \rho^2_k\gamma_k,\]

where $n$ is the number of components in the system, $m$ is the numbrer of precipitates, $N_{0i}$ is the number of moles of component $i$ in the matrix, $\mu_{0i}$ and $\mu_{ki}$ are the chemical potentials in the matrix and precipitate, $\rho_k$ is the radius of precipitate with index $k$, $\lambda_k$ is the elastic energy due to volume misfit between precipitate and matrix, $c_{ki}$ is the concentration of element $i$ in the matrix and $\gamma_k$ is the specific interfacial energy.

The dissipative terms are obtained with

\[ Q_1=\sum^m_{k=1}\frac{4\pi K_k\rho^2_k\dot{\rho}^2_k}{M_k},\]

\[ Q_2=\sum^m_{k=1}\sum^n_{i=1}\frac{4\pi I_k RT\rho^5_k\dot{c}^2_{ki}}{45c_{ki}D_{ki}},\]

\[ Q_3=\sum^m_{k=1}\sum^n_{i=1}\frac{4\pi O_k RT\rho^3_k \left( \dot{\rho}_{k}(c_{ki}-c_{0i}) +\rho_k \dot{c}_{ki}/3 \right)^2}{c_{0i}D_{0i}},\]

with $R$ being the gas constant, $D_{0i}$ and $D_{ki}$ being the diffusion coefficients in matrix and precipitate, $M_k$ being the interfacial mobility and $T$ absolute temperature. The shape parameter are finally obtained with

\[ S_k = 0.7631 h^{1/3}+0.3816 h^{-2/3},\]

\[ K_k = 0.2912 h^{2/3}+0.5824 h^{-1/3},\]

\[ I_k \approx 0.4239 h^{4/3}+0.6453 h^{-2/3},\]

\[ O_k \approx 1.0692 h^{2/3}.\]

The following figure shows the results of the analysis in graphical form, where the parameters are plotted as a function of the shape factor $h$.

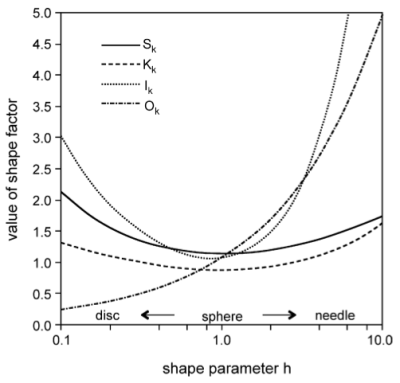Figure 2: Corrections to the growth rate of spherical precipitates that take into accound non-spherical shape (note that 'shape factor' in this figure refers to the values of $S_k$, $K_k$, $I_k$ and $O_k$)

Important note: In the practical implementation of the formulas into MatCalc, all quantities are normalized with respect to a sphere instead of the cylinder with $h=1$. This treatment assures that the calculations without shape factor and the simulations using a shape factor with value $h=1$ give identical results.

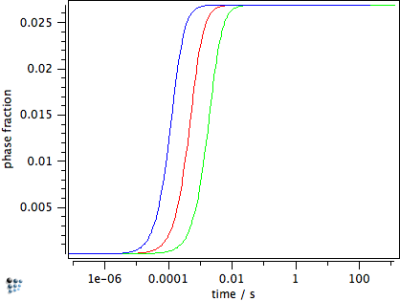
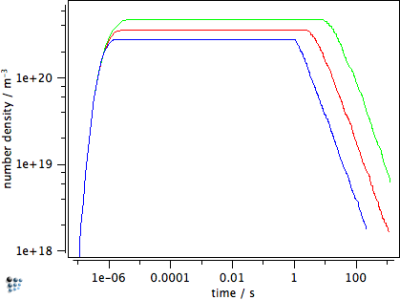
Finally, when calculating precipitate growth, this treatment delivers the result that growth of plate-shaped precipitates is fastest compared to spherical shape. Needle-shape is least favorable and is characterized by slowest growth rates. This is demonstrated for cementite particles of different shape factor in the figures below for the evolution of the phase fraction $f$, the mean radius $r$ and the number density $N$. In the figures, the red line corresponds to the calculation with $h=1$, the green line to needle shape with $n=10$, and the blue line to plate shape with $n=0.1$.

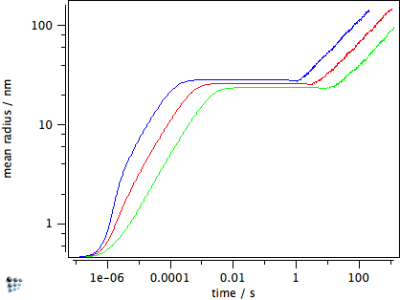Figure 3: Evolution of phase fraction, number density and mean radius for different values of $h$.

The figures above emphasize the fastest growth for plate-shaped precipitates, both in the phase fraction diagram as well as the mean radius. The needle-shaped precipitate grows slowest, however, it achieves the highest number density, since more nuclei are formed until supersaturation seizes and nucleation comes to a stop.

The geometry of non-spherical precipitates is uniquely defined by the combination of mean precipitate radius R_MEAN$phase and shape factor $h$. For analysis of the actual extension of the non-spherical precipitate, the mean precipitate diameter D_MEAN$phase and the two variables HEQ_MEAN$phase and DEQ_MEAN$phase for the equivalent height and equivalent diameter can be utilized. The following figure displays these quantities for the simulation of plate-shaped precipitates as performed in the previous section.

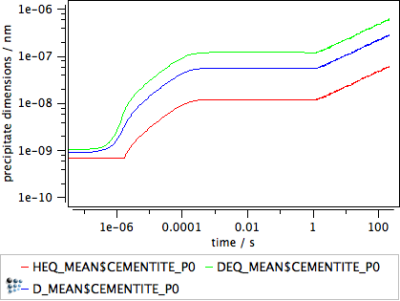Figure 4: Mean precipitate diameter of the spherical precipitate compared to the equivalent height and equivalent diameter of non-spherical precipitate. Note the implementation of the minimum precipitate radius for very small precipitates.

For larger precipitate sizes, the ratio between height and diameter corresponds exactly with the shape factor $h=0.1$. These variables can be used for comparison of simulations with experimental information.

Important note: Application of the shape factor is restricted by the setting for the minimum precipitate radius in the 'nucleation' tab of the 'phase status' dialog. By default, this value is 3.5e-10 m, which is approximately one atomic distance. If one of the two 'equivalent' quantities, height or diameter, reaches a value which goes below two times the minimum precipitate radius, MatCalc automatically fixes this value to the minimum size and adjusts the complementary quantity such that the volume of the non-spherical precipitate remains conserved.

This behavior of MatCalc is reflected in the diagram in the horizontal section for the equivalent diameter. Neither the equivalent radius, nor the diameter, can go below this limit.

Based on the distribution and the properties of the precipitates, MatCalc calculates the amount of precipitation strengthening according to the models discussed in the tech paper on precipitation strengthening. A major factor in the models underlying these calculations is the mean particle distance $\lambda$ between two precipitates on the glide plane of the dislocation. A classical expression of this kind for non-shearable precipitates is the Orowan strengthening model.

For the case of non-spherical precipitates, the deviation from spherical shape leads to a higher probability of a precipitate intersecting the dislocation glide plane. This reduces the mean distance $\lambda$ and, consequently, leads to a higher strengthening effect. This issue has been investigated in ref.³⁾, where a correction factor has been derived based on the definition of shape factor with $h=H/D$.

The basic assumption that has been made in this work is that the probability of finding a precipitate in a dislocation slip plane is given by the following simple model.

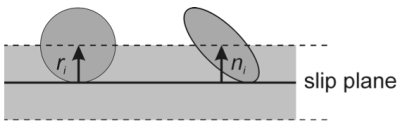Figure 5: Sketch for definition of non-spherical precipitates in evaluation of the mean particle distance for strength calculation.

For non-spherical precipitates, the angle between the slip plane of the dislocation and the precipitate orientation must be considered, as well as the precipitate shape factor $h$. Evaluation of these relations leads to a simple correction factor $K$ for the mean particle spacing $\lambda$ as

\[ K=h^{1/6}\cdot \left( \frac{2+h^2}{3} \right)^{-1/4}. \]

The critical yield strength attributable to precipitation strengthening then becomes

\[ \tau_\text{ell} = K^{-1}\cdot \tau_\text{sphere}.\]

The following figure, finally, displays the correction factor $K$ as a function of the shape factor $h$.

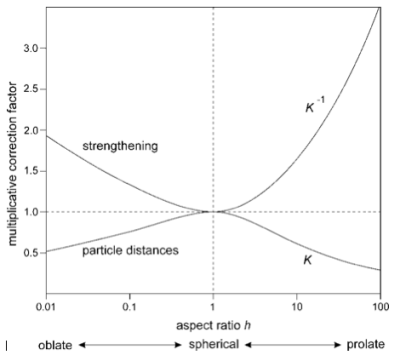Figure 6: Correction factor for the mean particle distance of non-spherical precipitates

The results suggest that the strengthening effect of non-spherical precipitates is generally more pronounced than the strengthening effect of spherical precipitates. The above relations are used by MatCalc as soon as use of the shape factor is selected in the 'precipitate' tab of the 'phase status' dialog.