Table of Contents
Primary precipitates
Compatibility
MatCalc version: 5.44 - …
Author: E. Kozeschnik
Created: 2011-11-14
Revisions:
Objectives
In this document, some strategies are discussed on how to treat primary precipitation in precipitation kinetics simulations in the solid state.
Related documents
Main document
Primary precipitates nucleate and grow in the residual liquid pockets before final solidification. They are usually significantly larger compared to secondary and tertiary precipitates. Due to their large size,1) primary precipitates occur in the microstructure commonly widely spaced and they do not contribute to precipitation strengthening. Primary precipitates are usually visible in optical light microscopy investigation. They might be potential nucleation sites for fatigue cracks under dynamic loading conditions.
Although primary precipitates are commonly not involved in the evolution of precipitation reactions after solidification due to their large size, they can potentially influence the chemical composition of the matrix (precipitation domain) by reducing the amount of available elements for precipitation after solidification. Consequently, some possibilities for taking this type of precipitates into account in MatCalc simulations are presented below.
The basic idea of the present treatment of primary precipitates is to introduce the primary precipitates by some method discussed below and keep them as part of the precipitation simulation, however, without nucleation of new particles of this type throughout the regular heat treatment. Thereby, the primary precipitates are fully involved in the precipitation process. They maintain mass conservation by binding the solute elements from the precipitation process in the residual liquid pockets. And it is also possible, though not likely, that they dissolve again and release the solute atoms into the matrix again.
Estimation of amount and size of primary precipitates
Primary precipitates are formed in the liquid state. The MatCalc precipitation models are not designed for liquid phase precipitation since its growth models have been developed for diffusion in the solid state. Convection and particle collisions in the liquid state are not accounted for. However, in order to take primary precipitation into account in the simulations, some workarounds can be applied to be able to account for this type of precipitates at least in an approximate way.
The most straightforward means to determine (or estimate) the amount of primary precipitation is the application of the Scheil-Gulliver model. It is described in some detail in the comprehensive example Thermodynamic equilibrium analysis for continuous casting simulation of micro-alloyed Fe-Al-C-N-Nb-Ti steel.
Introduce size distribution of primary precipitates
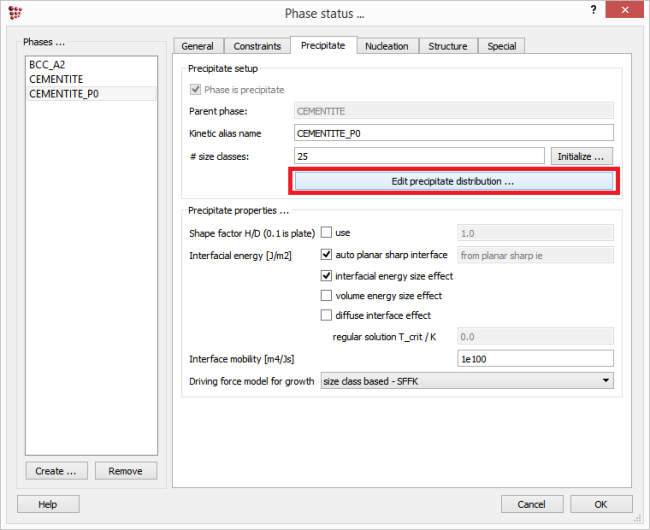
The size distribution, the phase fraction and the composition of the primary precipitates must in some way be entered into the MatCalc precipitation simulation scheme. There exist several ways for doing this: The recommended way is to generate distribution with the MatCalc routine, based on the composition and amount of the parent phase. This can by clicking on 'Edit precipitate distribution' button in 'Precipitate' tab of the 'Phase status' window. The user can also enter the size, number density and element mole fractions on various sites for each size class manually, but some caution is required by the parameter input, as explained below. The last way was the method of choice for the MatCalc versions older than 5.61 and relied on the performance of the 'virtual' heat treatment producing the desired distribution of primary precipitates directly from within a preliminary precipitation simulation.
Size distributions defined from parent phase
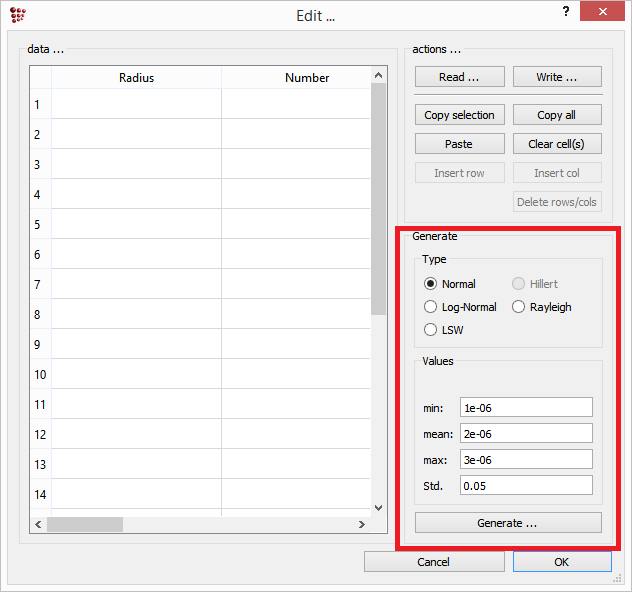
Starting from version 5.61, MatCalc allows to create size distribution for the precipitate phase. It follows a simple routine in which the required input values are:
- Phase fraction of the phase
- Values for minimal, mean and maximal radius for the precipitate
- Size distribution function
This feature can be accessed in ‘Phase status’ window. Select the relevant precipitate, switch to ‘Precipitate’ tab and click on ‘Edit precipitate distribution’ button.
On the left side of this window, a table is available which will contain the number density, radius and composition (in term of site fractions) data for each class of the phase. On the bottom right side, the distribution function for the size precipitates can be chosen and the data for the size range can be entered.
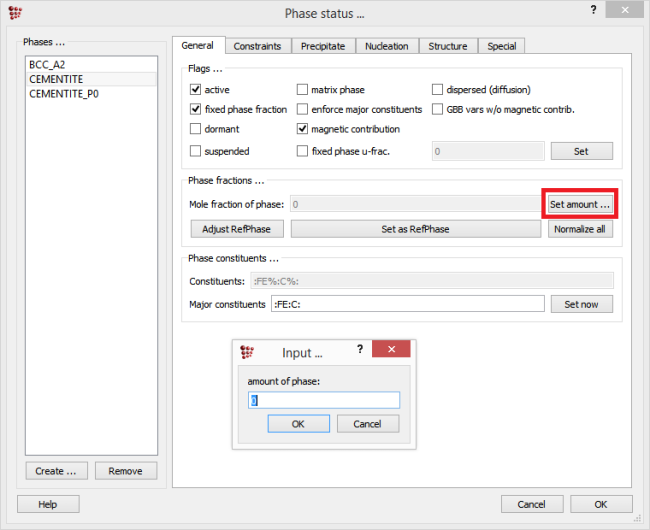
It must be noted that for the phase fraction, the value relevant for the parent phase of the precipitate (which is usually the equilibrium or the solidified phase) is taken. If needed, the phase fraction value can be modified by selecting the parent phase, switching to the ‘General’ tab, clicking on the ‘Set amount’ button and typing the value in the appearing window.
Starting from the Scheil-Gulliver analysis, the size distribution of the primary precipitate can be created simply by selecting the solidified phase (the one with ‘_S’-suffix) and creating a precipitate phase out of it. This procedure is demonstrated in Example P20-1: Treatment of primary precipitates.
Manually defined size distributions
When attempting to enter size distributions manually, please consider the following note.
Important …
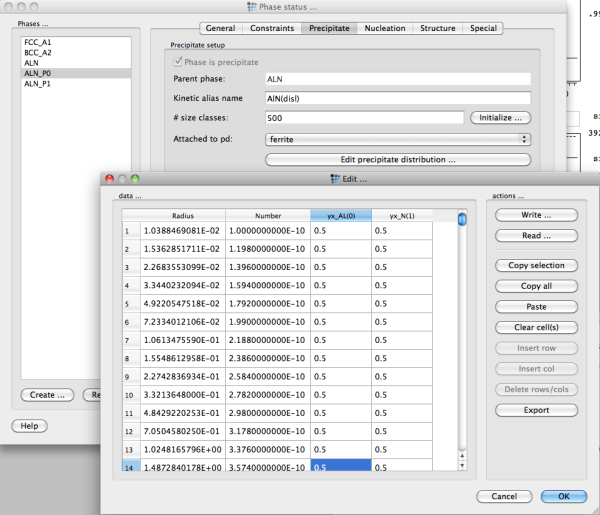
One major exception to this consideration is the special case of strictly stoichiometric precipitates. For instance, the Fe3C carbide in the Fe-C system has a fixed composition of three Fe atoms on one C atom, or the AlN precipiate in Fe-Al-N. For these simple cases, it is easily possible to maintain mass conservation and systems of this type are rather suitable for investigating the influence of size distributions on the precipitation behavior. In the download → utilities section of the MatCalc web site, an Excel sheet (MatCalcDistributions.xls) is provided that facilitates the generation of typical idealized size distributions (Gaussian, log-normal, LSW). This spread sheet generates the distribution data for 500 size classes, which can be transferred into MatCalc using Copy and Paste.
After generation of the size distribution in some pre-processing, e.g. the MatCalcDistributions.xls sheet, the values for number, radius and chemical composition of each size class can be entered in the precipitate distribution dialog of the phase status → precipitate dialog. Note that the chemical compositions are entered in yx-variables, which means that all yx site fractions over all sublattices sum up to one.
It is most convenient to copy and paste the values into MatCalc. Make sure that you have initialized your precipitate with sufficient number of size classes, otherwise the paste procedure will fail.
Size distributions from virtual pre-treatment
For complex precipitates, manual input of size distributions is not recommended for the reasons explained above. Instead, size distributions with some desired mean precipitate radius can be generated in a 'virtual' pre-treatment, with the term 'virtual' emphasizing that these pre-treatments can involve any simulation setup that generates the desired distribution regardless of whether the input parameters are based on physical grounds or not.
These pre-treatments are commonly performed in the following steps:
- Set up the precipitation system, create precipitate phases and precipitation domains.
- Create an additional precipitation domain for the pre-treatment.
- Create an additional precipitate population for the primary precipitate. Use the 'prec_name_p0' for the primary precipitate and 'prec_name_p1' (and higher index) for secondary, tertiary etc. precipitates.
- Select the 'restrict nucleation to prec domain' option in the nucleation tab of the phase status dialog to link the '_p0' precipitate to the precipitation domain of the pre-treatment. Let the other precipitates nucleate in the precipitation domains of the regular heat treatment.
- Design the pre-treatment such that after executing the pre-treatment, the '_p0' population of the primary precipitate has the desired phase fraction and mean radius.
The last step in this recipe is the most important one, and there are several strategies on how to design this virtual pre-treatment most efficiently in terms of computational effort. Minimum simulation time for pre-treatments can be achieved, if time-consuming coarsening regimes are avoided, as well as long continuous cooling segments, where nucleation of precipitates can also make the computation times longer than necessary. A simple methodology for designing efficient pre-treatments is as follows:
- In a preliminary step, perform a Scheil-Gulliver simulation to determine the type and amount of primary precipitates in your system. See the example E20 - Thermodynamic equilibrium analysis for continuous casting simulation of micro-alloyed Fe-Al-C-N-Nb-Ti steel for instructions on how to do this.
- Remember the amount (phase fractions) of your primary precipitates as well as their approximate chemical composition. This is also elaborated and discussed in the example E20.
- Set up an equilibrium simulation involving only the thermodynamic equilibrium phases of the precipitation domain and the primary precipitates. Perform equilibrium simulations to find out at which temperature the phase fraction of the primary precipitate fits the phase fraction determined previously in the Scheil-Gulliver simulation. Check whether the chemical composition of this phase corresponds roughly to the primary precipitate composition determined in the Scheil-Gulliver step.2)
- Set up your full precipitation system as described above for the virtual pre-treatment. It is important that you create all precipitation domains and precipitates for the following real heat treatment. We want to save the calculation state after pre-treatment and use it as a starting condition for the real heat treatment but we can only load these states correctly if the number and type of phases and precipitation domains are unchanged.
- Create a 'pre-heat treatment' in the heat treatment dialog. Define the segments as suggested below.
In principle, the segments of the virtual pre-treatment and all temperatures, holding times and cooling/heating rates can be defined as you like. Fully arbitrary. Also, the settings for the pre-treatment precipitation domain and the primary precipitates can be set entirely without consideration of physical principles. However, in the context of computational efficiency, there are numerous more or less successful strategies possible. The one suggested below has proven to perform reasonably well in many practical investigations. It is described in detail in the next section.
Design of a computationally efficient virtual pre-treatment
The two main achievements of a successful pre-treatment are to produce an initial distribution of (primary) precipitates that have the desired values for
- phase fraction and
- mean precipitate radius.
The phase fraction of primary precipitates is commonly obtained from the preliminary equilibrium calculation as described above. The mean radius is commonly observed from light optical or electron microscopy. Its value is usually in the order of a few µm.
In the virtual pre-treatment, these two quantities can be efficiently adjusted in the following multi-stage heat treatment:
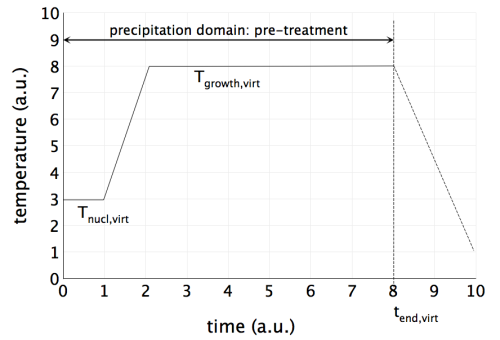
- For only a few seconds, run the pre-treatment at an isothermal temperature $T_\text{nucl,virt}$, where nucleation of primary precipitates occurs in such a number that, in the subsequent growth step, the desired size can be achieved without entering the coarsening stage.
- For adjustment of the desired number density, first of all adjust the nucleation sites of the primary precipitates in the nucleation tab of the phase status dialog. By this procedure, you modify the constant $N_0$ of the nucleation rate expression by several orders of magnitude. Often, 'grain boundary corners' are suitable for the purpose of virtual pre-treatments for primary precipitates.3) For fine-tuning of the results, you might want to modify the nucleation constant. Decrease its value if the precipitates remain too small, increase it if they become too large. Do not worry if $N_C$ adapts rather large or small values. This is allowed since we design a virtual treatment in this step, and not a real precipitation simulation.
- At heating rates in the order of 100 K/s, move to the temperature $T_\text{grow,virt}$ determined in the preliminary equilibrium calculation, which has been pre-evaluated in order to produce the desired phase fraction. Run the simulation isothermally at this temperature just as long as you need to reach the equilibrium phase fraction at $T_\text{end,virt}$.4)
The following screen shot displays a typical pre-treatment for primary TiN precipitation in micro-alloyed steel.
The end time of the virtual pre-treatment $t_\text{end,virt}$ is commonly defined by point where the growth stage for your primary precipitates is completed. You can observe this point easily in the corresponding plots for phase fraction, mean radius and number density.
The actual distribution of your primary precipitates can be inspected in the precipitate distribution - histogram plot. In the early stages, directly after reaching the phase fraction maximum, the distribution is often rather small. If you want to start your simulation with a wider initial distribution, increase the simulation time a bit, such that you enter the coarsening regime. By this method, you will be able to adjust the width of your precipitate distribution.
Transfer results / size distribution
Once you have generated a size distribution of your primary precipitate(s) in the virtual treatment, you have two options to carry on.
- Save the size distribution into a calc state. Use this state as a starting condition for further precipitation simulation.
- Export the size distribution into a file. Read the distribution file and import it into any independent further computation.
Both ways are demonstrated in the example P20 (Example P20: Precipitation simulation during continuous casting of micro-alloyed Fe-Al-C-N-Nb-Ti steel, part 1: Treatment of primary precipitates).