Table of Contents
TechPaper #2011003: The CNT multi-component transient nucleation rate
Compatibility
MatCalc version: 5.40 - …
Author: E. Kozeschnik
Created: 2011-06-27
Revisions: 2018-04-09 E. Kozeschnik for version 6.01
Objectives
This paper discusses the implementation of the multi-component transient nucleation rate expression in the MatCalc precipitation kinetics framework. The equations presented below are derived in the framework of Classical Nucleation Theory (CNT) and they are strictly valid only for the special case of size-independent interfacial energy and volume free energy as well as homogeneous nucleation. The MatCalc-specific extensions (size effect/diffuse interface effect/volume energy effect) and their implementation are described in seperate documents.
Related documents
Main document
Nucleation in MatCalc is realized in an extended Classical Nucleation Theory framework, where all input quantities are either given from experimental information (microstructure parameters such as dislocation density and grain size) or from theory (such as chemical driving force and interfacial energy). For details on the theoretical models, see the corresponding section in the list of MatCalc-relevant publications.
Energetics of nucleus formation
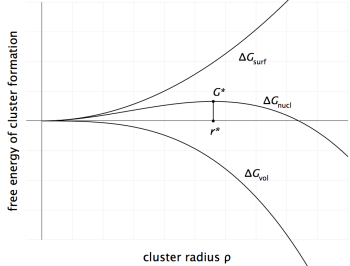
If a nucleus of a new phase forms, the total change in energy $\Delta G_\text{nucl}$ accompanying this event can be expressed as
\[ \Delta G_\text{nucl} = \frac{4\pi}{3} \rho^3 \cdot \Delta G_\text{vol} + 4\pi \rho^2 \gamma\]
where $\rho$ is the radius of the nucleus, $\Delta G_\text{vol}$ is the volume free energy change on nucleation and $\gamma$ is the specific interfacial energy. $\Delta G_\text{vol}$ has negative value if the phase to form is thermodynamically stable. The function $\Delta G_\text{nucl}$ is shown in the next figure as a function of the nucleus radius.
From this relation, the extremum value for the critical radius $\rho^*$ can be evaluated after setting the first derivative of $\Delta G_\text{nucl}$ to zero with
\[ \frac{\partial}{\partial \rho}\Delta G_\text{nucl} = 0\]
The critical radius is then
\[ \rho^* = -\frac{2\gamma}{\Delta G_\text{vol}} \]
and the critical nucleation energy is
\[ G^* = \frac{16\pi}{3} \frac{\gamma^3}{(\Delta G_\text{vol})^2} \]
The transient nucleation rate
The number of newly formed precipitates per unit volume and unit time is given by the transient nucleation rate $J$ as
\[J=N_0Z\beta^*\exp\left({-\frac{G^*}{k_\text{B}T}}\right)\exp\left({-\frac{\tau}{t}}\right)\]
where $N_0$ is the number of potential nucleation sites, $Z$ is the Zeldovich factor, $\beta^*$ is the atomic attachment rate, $G^*$ is the critical nucleation energy, $k_\text{B}$ is the Boltzmann constant, $T$ is the absolute temperature, $\tau$ is the incubation time and $t$ is time.
Multi-component CNT expressions
It is important, now, to realize that all quantities in the nucleation rate expression are defined either from independent experimental information (e.g., diffusion coefficients) or given in terms of some theoretical model (e.g., chemical driving force and interfacial energy). The table below summarizes all the quantities entering the transient nucleation rate expression.
| Symbol | Expression | comment |
|---|---|---|
| $N_0$ | / | Number of potential nucleation sites |
| $Z$ | \[{\left[-\frac{1}{2\pi k_\text{B}T}\left( \frac{\partial^2 \Delta G_\text{nucl}}{\partial n^2} \right)_{n^*} \right]^{\frac{1}{2}}}\] | Zeldovich factor |
| $\beta^*$ | \[ \frac{4\pi \left(\rho^* \right)^2}{a^4 v^\alpha} \left[ \sum_{i=1}^{n}{\frac{\left(c_{ki}-c_{0i}\right)^2}{c_{0i}D_{0i}}} \right]^{-1} \] | Atomic attachment rate |
| $\tau$ | \[\frac{1}{2\beta^* Z^2} \] | Incubation time |
| $G^*$ | \[\frac{16\pi}{3} \frac{\gamma^3}{\left(\Delta G_\text{chem}+\Delta G_\text{el} \right)^2} \] | Critical nucleation energy |
| $\rho^*$ | \[ -\frac{2\gamma}{\left(\Delta G_\text{chem}+\Delta G_\text{el} \right)} \] | Critical nucleation radius |
| $\Delta G_\text{nucl}$ | \[ \frac{4\pi}{3}\rho^3 \cdot {\left(\Delta G_\text{chem}+\Delta G_\text{el} \right)} + 4\pi \rho^2 \cdot \gamma\] | Total energy change on nucleation |
| $\Delta G_\text{chem}$ | \[ \sum^n_{i=1}{X^{\beta}_i(\frac{\mu^{\beta}_i}{v^\beta}-\frac{\mu^{\alpha}_i}{v^\alpha})} \] | Volume free energy change on nucleation (=negative chemical driving force) |
| $\Delta G_\text{el}$ | \[ \frac{E}{1-\nu_\text{P}} \cdot \left( \epsilon^* \right)^2\] | Elastic strain energy, see also document Heterogeneous nucleation |
| $\gamma$ | \[ \frac{n_\text{S} \cdot z_\text{S,eff}}{N_\text{A} \cdot z_\text{L,eff}} \cdot \Delta H\] | Interfacial energy, see document Evaluation of interfacial energies for details |
The expressions above are valid for spherical precipitates.