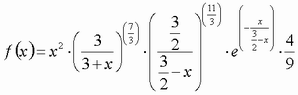Table of Contents
T14: Introduction to precipitation calculations
This tutorial was tested on
MatCalc version 6.04 rel 1.001
license: free
database: mc_fe.tdb; mc_fe.ddb
Complimentary files
Click here to view the script for this tutorial
Contents:
- Precipitation of cementite in a ferritic matrix in Fe-0.2 wt.% C
- Creating a precipitation domain
- Creating a precipitate phase
- Mobility and physical data
- Plotting and interpreting calculation results
Setting up the system
A. Thermodynamic setup
The first step is to set up the thermodynamics of the system. In the new workspace, open 'Global > Databases' and select the elements Fe and C. For a precipitation calculation, it is only necessary to include the phases which are directly involved in the precipitation, i.e. the precipitating phase and the matrix in which it forms. This example considers the precipitation of cementite in ferrite, so the two phases to be selected are BCC_A2 and CEMENTITE. When the thermodynamic data have been read in, open 'Global > Composition' and enter the carbon content of 0.2 wt.%.
B. Precipitation domain
The next two steps are to define and configure the precipitating phase and the domain in which it will form. These two steps can be done in either order. In this example, the precipitation domain will be set up first.
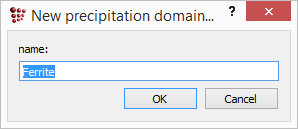
Open 'Global > Precipitation domains' and click on the 'New' button towards the bottom left. A box will appear, prompting for a name for the new domain. Any name can be chosen here, for example 'Ferrite' or 'Matrix' and click 'OK'.
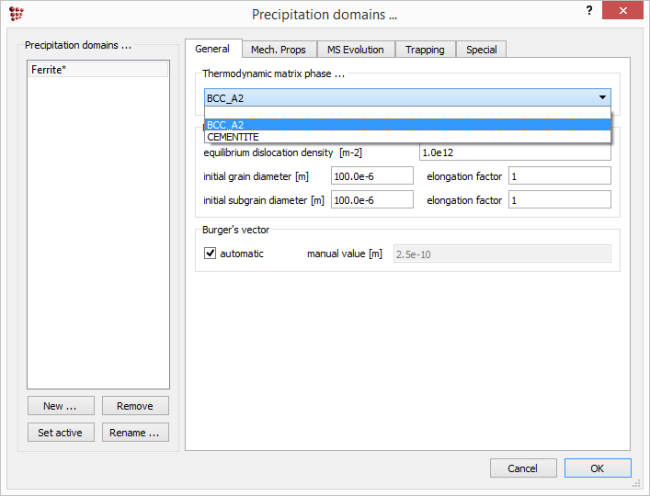
On the 'General' tab → 'Thermodynamic matrix phase', choose 'BCC_A2' from the drop-box to associate this phase with the newly defined domain. Leave the rest of the settings as they are, and click 'OK'.
C. Precipitate phase
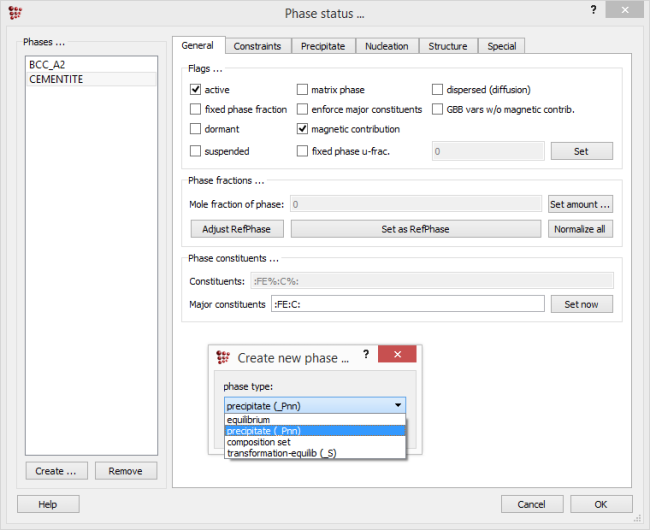
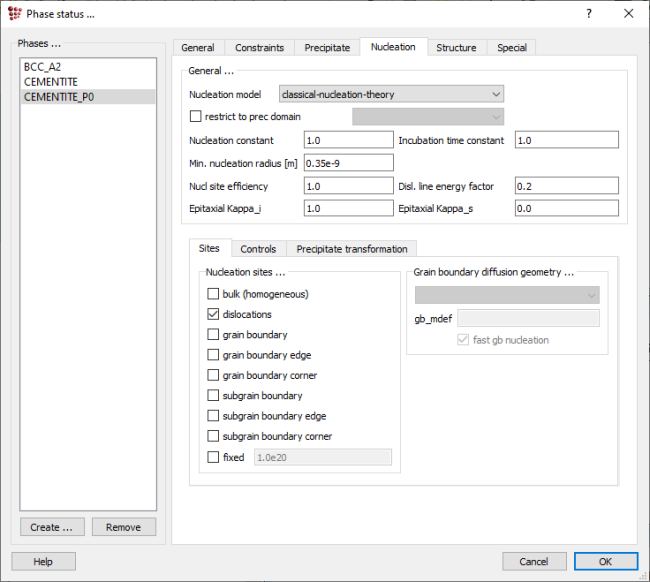
To create the precipitate phase, open 'Global > Phase status'. In the 'Phases' list on the left-hand side, select 'CEMENTITE' and click on 'Create'. Select 'precipitate (_Pnn)' from the drop box which opens.
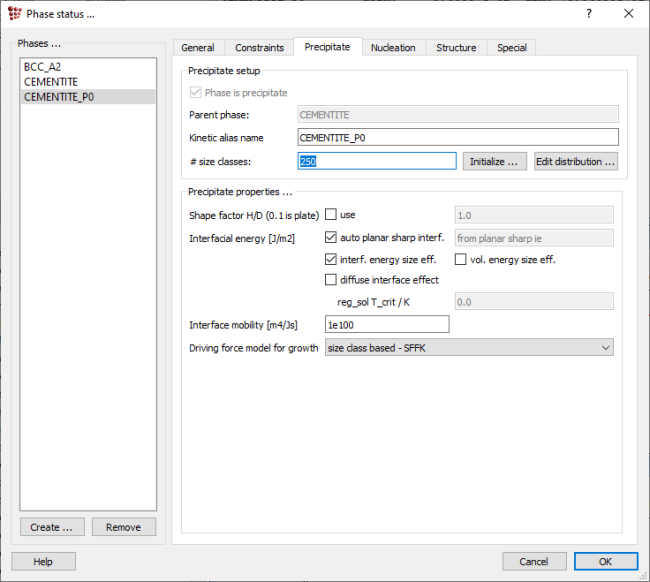
A new phase, CEMENTITE_P0 appears in the phase list; click on this to select it. Open the 'Precipitate' tab, and enter '250' in the '# size classes' box, click on 'Initialize' and accept the warning message. The precipitates are considered as belonging to a number of classes of particles with the same radius and composition. Classes are created, rearranged and deleted during the calculation, allowing simulation of the precipitate size distribution.
The choice of the number of classes represents a trade-off between calculation time and required precision. If only average properties, such as the mean precipitate radius, are of interest, then it is sufficient to use a small number of classes such as 10 or 20. By contrast, to obtain the best possible simulation of size distribution, the number of classes should be increased to a higher value, such as 250 as used here. Leave all the other settings in this tab as they are.
Open the 'Nucleation' tab and select the 'Sites' sub-tab. In the 'Nucleation sites…' part of this tab, remove the check mark by 'bulk (homogeneous)' and instead click in the box beside 'dislocations' . Click on 'OK' to save these settings and return to the main screen.
D. Loading mobility data
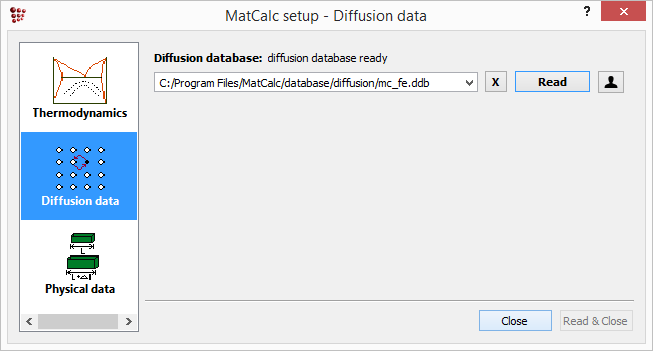
Simulations of precipitation require not only thermodynamic data (already loaded in step A) but also mobility data, from which the diffusivities of the elements in the phases can be calculated. Read in the mobility data by opening 'Global > Databases' and select 'Diffusion data' on the left side. Click on 'Read…' and open 'mc_fe.ddb' database. Click on 'Close'
E. Creating plots for the output
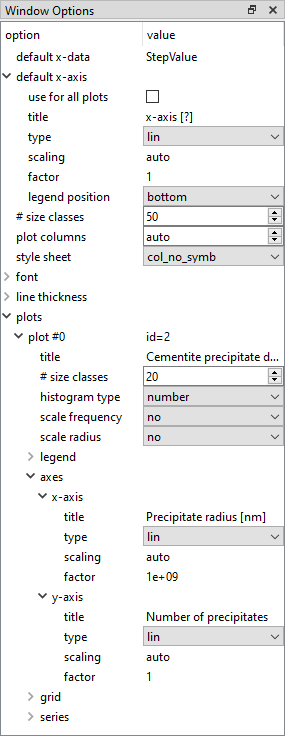
Create a new 'Plot: XY-data' window. Drag and drop 'F$CEMENTITE_P0' from the variables window to this plot. In the 'options' window, set 'default x-axis' to 'log' type. Change the title of 'default x-axis' to 'Time [h]' and the factor to '1/3600' to convert seconds into hours. The title of the 'plot #0' should also be changed to 'Phase fraction of cementite precipitates' and the title of y-axis to 'Phase fraction'.
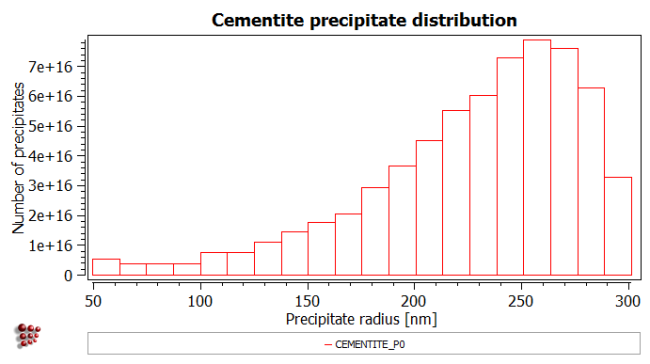
Next, create a new window 'Plot: precipitate distribution - histogram' (p5) window. Select 'CEMENTITE_P0' from the box which opens and click 'OK'. In the 'options' window, change the number of '# size classes' for this histogram to '20'. Switch off the default x-axis (in 'default x-axis', set 'no' for 'use for all plots') and set the x-axis label to 'Precipitate radius [nm]'. In the 'factor' line for this x-axis, enter '1e9'. This expresses the particle radii in nanometres instead of metres, making the scale easier to read. Change the y-axis label to 'Number of precipitates'.
Both the histogram and the plot of phase fraction against time are updated during the calculation, so it is possible to follow the evolution of the size distribution and the phase fraction as the calculation takes place.
The calculation
As the introduced number of classes is quite large (as defined in p. 1.D.), it will be beneficial to modify the algorithm used for the calculation. To do this the numerical limits describing the increase of the nucleation density in the 'convergence control' field should be changed. Up to now, this can be only modified via console commands. Type the following command-line in the console:
set-simulation-parameter nucleation-density-increase-factor=1,05
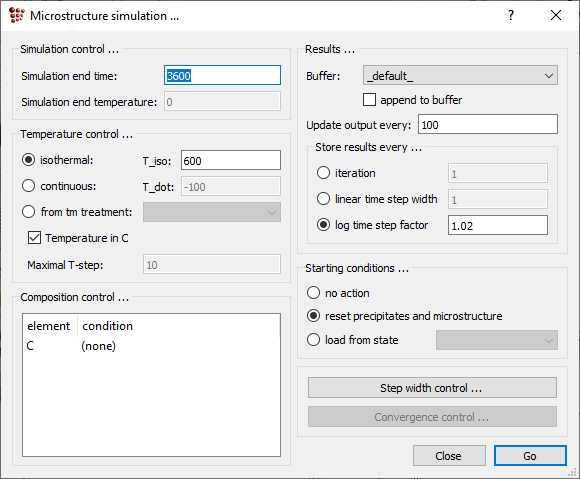
Open 'Calc > Microstructure simulation' or click on the ![]() icon (keyboard shortcut: 'Ctrl + K'). Enter '3600' as the simulation end time. This is in seconds, so is equivalent to 1 hour. Note that in the 'Temperature control' section, an isothermal heat-treatment at 600°C has been selected by default; leave this setting as it is.
icon (keyboard shortcut: 'Ctrl + K'). Enter '3600' as the simulation end time. This is in seconds, so is equivalent to 1 hour. Note that in the 'Temperature control' section, an isothermal heat-treatment at 600°C has been selected by default; leave this setting as it is.
To give more frequent updates of the graphs on the screen, the 'Update output every' number can be decreased from 100 to 50. However, this will slow down the calculation somewhat, so it is probably not advisable on slow machines. Leave the other settings as they are, and click on 'Go'.
The information in the 'Output' window gives a summary of the current system composition, simulation time
******** isothermal,T=873.16 K (600 C) *************************************
1, recs=1; its=1/1, dt=1e-012, time: 1e-012s (2.778e-016h), eps_dot=0, T=600 C (873.1 K)
#Ferrite: BCC_A2, sv=1,77e-010 (sve=1,77e-010), dcf=1, ro=1e+12, gsc=0 (dt=0, -/-1)
FE +9.90768e-001(+0.00e+000) C +9.23192e-003(+0.00e+000)
———————————————————————————————————-
CEMENTITE_P0: FE75C25, nucl-site: d, nucl-dfm=6825,5, n_dot=0,0, ans=4e+021 (dt=0, -/-1)
+ CEMENTITE_P0 precipitation started at 1.9531e-008 s, T=600 °C (873.15 K)
- First line:
1 -Number of iterations.
recs -Number of records in buffer.
dt -Last time step.
time -Absolute simulation time in [s].
eps_dot -Strain rate in [s-1].
T - Current temperature in [°C] (in [K]).
- Second line:
#Ferrite - Precipitation domain, BCC_A2 - matrix phase,
sv - current vacancy concentration
sve - equilibrium vacancy concentration
dcf - diffusion correction factor due to the presence of the excess vacancies
ro - current dislocation density
gsc - number of grain classes used (meaningful for multi class grain growth model)
damping feature (dt=0,-) - maximum time step allowed due to the matrix condition
- Third line:
FE +9.90768e-001(+0.00e+000) - Composition of matrix
- Fourth line:
CEMENTITE_P0: - precipitate phase
FE75C25 - composition of the most stable nuclei
nucl-site - nucleation sites
nucl-dfm - driving force for nucleation in [J/mol]
n_dot - nucleation rate
ans - available nucleation sites
- Last line:
+ nucleation of CEMENTITE_P0 started at 1.9531e-008 s, T=600 °C (873,15 K) - Additional information: Nucleation started '+' or stopped '-' and the exact system parameters at that time.
Another output result, at a later stage:
******** isothermal, T=873.16 K (600 C) ************************************
2500, recs=291; its=1/1, dt=0,0062724, time: 18,7583s (0,005211h), T=600 C (873,2 K), on Tue, 17:49:51
#Ferrite: BCC_A2, sv=1,77e-010 (sve=1,77e-010), dcf=0, ro=1e+012, gsc=0 (dt=0, -/-1)
FE +9,99771e-001(+0,00e+000) C +2,28862e-004(+0,00e+000)
———————————————————————————————————-
CEMENTITE_P0: (250/.-gs/1e+020/d) f=0,03605/rm=3,94e-008/dfm=60,2,nucl-dfm=60,2(FE75C25)
FE75C25, n_dot=0e+000 (ecdf=1), ans=0, mcomp(its:6), step: (dt=1e-005, rad-shrink/249)
- Additional information for the existing precipitate
(0/..gs/0e+00/d) - number of classes used / '+', '-' or '.', meaning: New class built, class deleted or no change; 'g' or 's' precipitate in classes are growing or shrinking / number of precipitates / nucleation sites
f - mole fraction of precipitate phase
rm - mean radius of precipitate phase
dfm - driving force (chemical) for formation of phase in [J/mol]
dt - maximum time step allowed due to the precipitate condition
The carbon content of the matrix has decreased from 9.2×10-3 initially (iteration 1) to 2.3×10-4 in iteration 2500. The precipitate phase uses 250 classes and consists of roughly 1×1020 particles. The mole fraction of cementite in the matrix is 0.03605 (3.6%). There is a small positive driving force for nucleation (60 J) and the nucleation rate (n_dot) is zero. This is because all nucleation sites are saturated (ans=0).
To avoid numerical instability, unreasonably large changes, for example in composition, precipitate volume, precipitate number or driving force, are prevented. Here, the coarsening stage is in progress and small particles are shrinking. A maximum value of radius reduction per time-step is imposed (rad-shrink); this reduces the time-step to 1e-5 s for the next step. The calculation speed can be increased by setting the windows to 'manual update' so that the graphs are not updated. Select 'View-Freeze update' or press 'Ctrl+I' to freeze the currently selected window. The same procedure unlocks the window again. To update the window content, press 'Ctrl+U' or select 'View > Update all window contents'.
Interpreting the results
Nucleation, growth and coarsening
When the calculation is finished, add three new plots in the same window as the plot of F$CEMENTITE_P0 versus time. Drag and drop NUM_PREC$CEMENTITE_P0 (number of cementite precipitates) into the first of these, NUCL_RATE$CEMENTITE_P0 (nucleation rate) into the second. In the third, add R_MEAN$CEMENTITE_P0 (mean radius), R_CRIT$CEMENTITE_P0 (critical radius), R_MIN$CEMENTITE_P0 (minimum radius) and R_MAX$CEMENTITE_P0 (maximum radius). These variables can be found under 'kinetics: precipitates' and 'kinetics: nucleation' in the 'variables' window.
Type in the following settings for the plots:
1. Plot 1
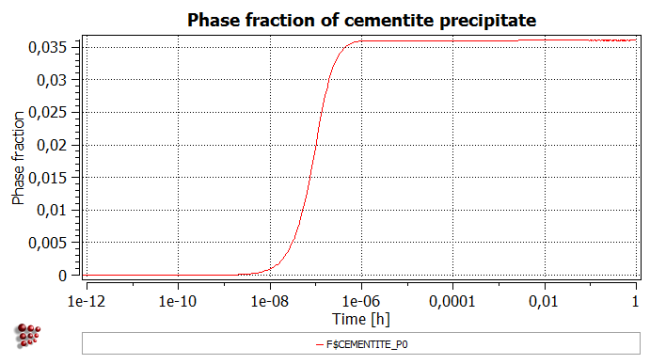
- Title: 'Phase fraction of cementite precipitate'
- Y-axis title: 'Phase fraction'
2. Plot 2
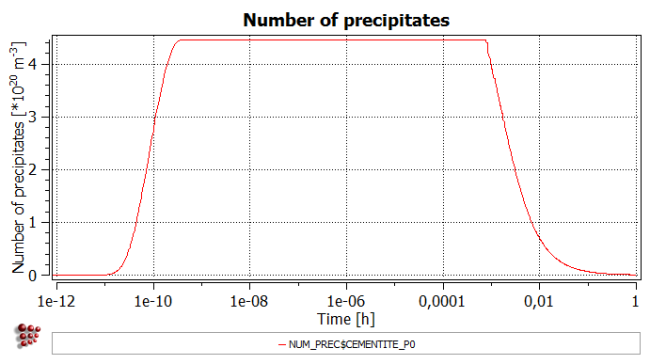
- Title: 'Number of precipitates'
- Y-axis title: 'Number of precipitates [*10<sup>20</sup> m<sup>-3</sup>]'
- Y-axis factor: '1e-20'
3. Plot 3
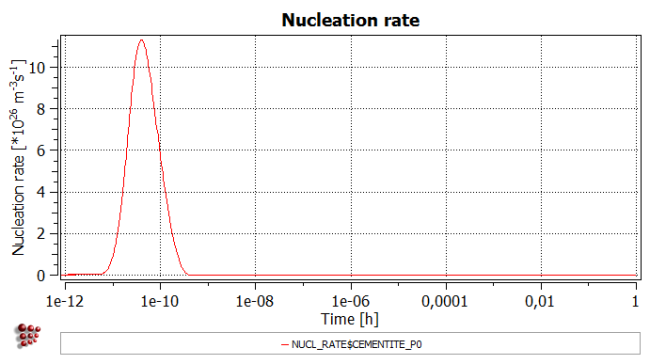
- Title: 'Nucleation rate'
- Y-axis title: 'Nucleation rate [*10<sup>26</sup> m<sup>-3</sup>s<sup>-1</sup>]'
- Y-axis factor: '1e-26'
4. Plot 4
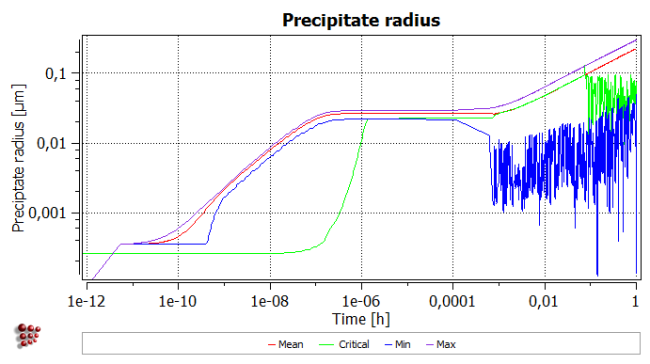
- Title: 'Precipitate radius'
- Y-axis title: 'Precipitate radius [<html>μ</html>m]'
- Y-axis type: 'log'
- Y-axis factor: '1e6'
5. Default x-axis
- Use for all plots: yes
- Title: 'Time [h]'
- Type: 'log'
- Scaling: '1e-12..'
- Factor: '1/3600'
Note the usage of the html-tags for the text with special features:
- the text between the '<sup>' and '</sup>' tags will be displayed as superscript (e.g. 10<sup>20</sup> appears as 1020)
- '<html>μ</html>' is used to display the Greek letter $\mu\$
Using these plots, the different stages of nucleation, growth and coarsening can be identified.During the nucleation stage, between 1e-11 and 1e-9 hours, the number of precipitates increases rapidly, but since these precipitates are, as yet, extremely small, the phase fraction of cementite also remains small. During this stage, the nucleation rate rises initially, due to a positive driving force for nucleation, and decreases again to zero when all the available nucleation sites are occupied.
The next stage, from approximately 1e-9 to 1e-6 hours, is the diffusion-controlled growth of these nuclei; this continues until the equilibrium phase fraction of cementite reaches its equilibrium value, as indicated by the plateau on the 'Phase fraction' curve. The number of precipitates does not change during this stage, but there is an increase in radius which can just be detected on the plot below. There follows a period in which there is little or no change in any of the three parameters.
Finally, at just over 1e-2 hours onwards, there is the onset of coarsening, which is characterised by a decrease in the number of precipitates accompanied by an increase in radius. The critical radius rises and becomes larger than the smallest precipitate classes. Therefore these classes start to dissolve and the newly available carbon is used to grow the larger precipitates (Gibbs-Thomson effect). The minimum radius is unstable (leading to a 'noisy' appearance on the graph) as the small precipitates are shrinking (minimum radius goes down) and dissolving (minimum radius goes up to the next smallest class present in the system).
Histograms of precipitate size distribution
The plot above shows only the variation of the mean radius with time, but more detailed information on the distribution of particle sizes can be found on the histogram. At the end of the calculation, the final size distribution is shown on the histogram. The distribution at other stages of the calculation can be recalled using 'Global > Buffers > Edit buffer states'. This brings up a list of all the states saved in the memory, with details of time, temperature and time-step. Selecting one of these records loads the corresponding particle size distribution into the histogram if the 'auto load' box at the bottom left is ticked. Otherwise, it can be loaded by clicking on the 'load selected' button.
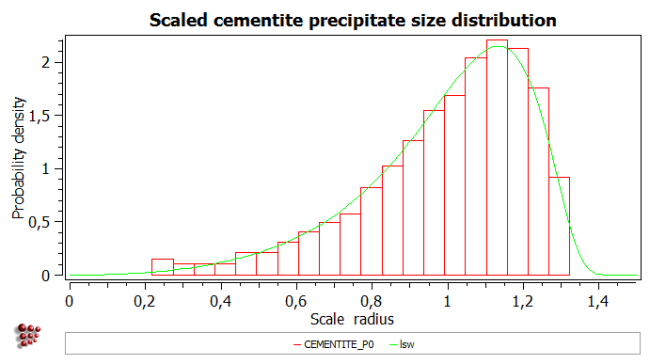
In the final part of this tutorial, the precipitate size distribution as calculated by MatCalc will be compared with the Lifshitz-Slyozov-Wagner (LSW) distribution given by the following equation:
In the histogram window, create a new plot and add a new series for it (set 'CEMENTITE_P0' for 'phase'). In the options under 'plots', select 'density' for 'scale frequency' and 'yes' for 'scale radius'. Name x-axis as 'Scaled radius' and the y-axis as 'Probability density'. Set the scaling of the x-axis as '0..1.499' because the LSW function is only defined between 0 and 1.5.
Enter the LSW function, either using the 'Functions and Variables' box or by using the following command-line in the console:
set-function-expression function=lsw expression=x^2*(3/(3+x))^(7/3)*((3/2)/(3/2-x))^(11/3)*exp(-x/(3/2-x))*4/9
Then add the function to the scaled plot, either using the right-click menu in the Options window to add a new 'function/expression' series (as it was done in Tutorial 6) or by using the following command-line:
set-plot-option . s n f LSW 0..1.5
The plot below shows a comparison between the LSW function and the histogram simulated by MatCalc.
Consecutive articles
The tutorial is continued in article T15 - Effect of microstructure and conditions (Part 1)
Go to MatCalc tutorial index.