Table of Contents
T21: Strain induced precipitates
This tutorial was tested on
MatCalc version 6.04 rel 1.002
license: free
database: mc_fe.tdb; mc_fe.ddb
Complimentary files
Click here to view the script for this tutorial
Contents:
- Effect of volumetric misfit on precipitation kinetics
- Introduction of deformation into the thermo-mechanical treatment
- Effects of the applied deformation on the precipitation kinetics
Deformation process influences the microstructure of the alloy. One of the effects is the occurence of the strain induced precipitates. This tutorial demonstrates how the deformation processes can be included in the simulation of the processed material. Moreover, the effects of the deformation on the precipitation kinetics are demonstrated and discussed.
Setting up the system
Create a new workspace and open the 'mc_fe.tdb' database. Select the elements 'Fe', 'Nb' and 'C', together with the phases 'BCC_A2', 'FCC_A1' and 'Cementite'. Click on 'Read' instead of 'Read & Close', as the subsequent step is to read the diffusion database in this window. Select 'Diffusion data' on the left side and read the 'mc_fe.ddb' database. Enter the composition of 0.2 wt.% C and 0.04 wt.% Nb. In menu 'Calc', click on 'Set start values' and calculate an equilibrium at the initial 1000°C.
Phase solubilities
In order to have some insight into the system equilibria, perform a stepped equilibrium calculation. In 'Stepped euilibrium ' window select the temperature range of 400-1400°C with the step of 10°C. Click on 'OK'
The phase fractions can be plotted by calling the appropriate user-defined window. In 'View' → 'Create new window', select the 'user defined' tab. There, select '01_all_phase_fractions over T_celsius_logY' and click on 'OK'.
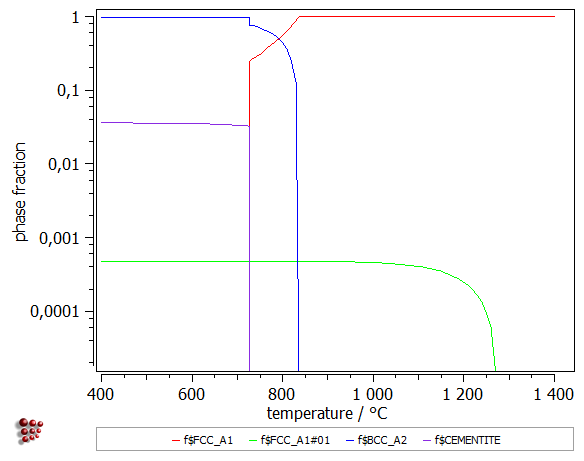
This will result in the plot looking like the one shown below. From this diagram it can be concluded that NbC precipitates below 1300°C and the ferrite will form below 850°C.
Precipiation domains and phases
Next, create a precipitation domain called 'austenite' in the 'Precipitation domains …' window. Select FCC_A1 as the thermodynamic matrix phase.
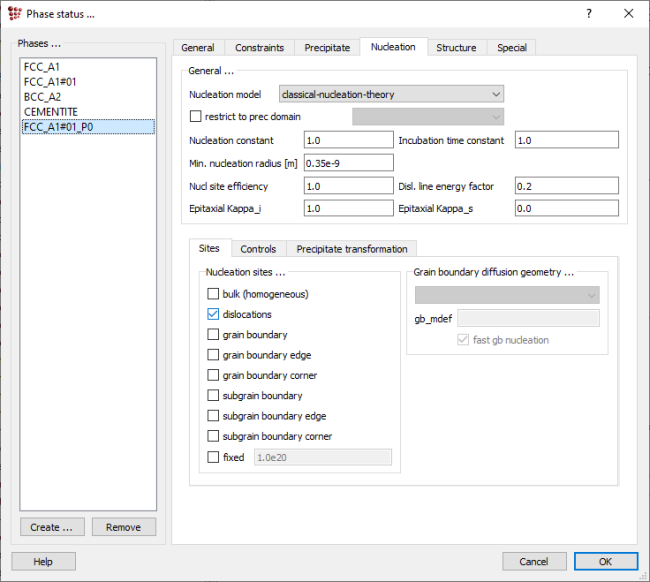
Now, define the precipitate phase settings in 'Phase status' window. Select 'FCC_A1#01' and click on 'Create' and 'precipitate (_Pnn'). In 'Nucleation' → 'Sites' set 'dislocations' as nucleation sites (and remove the checkmark from 'bulk').
Thermo-mechanical treatment
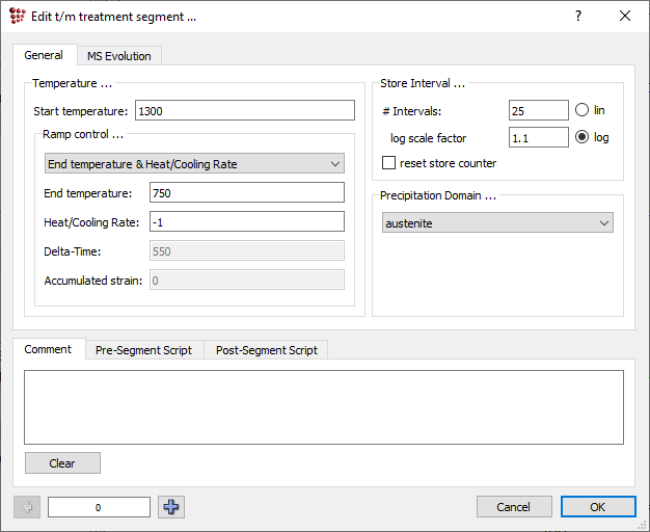
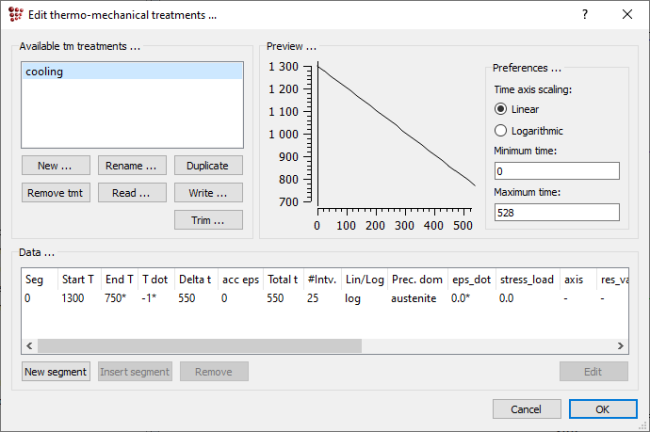
The last step before the initial kinetics simulation is the definition of the thermo-mehanical treatment. In 'Global' → 'Thermo-mech. treatments …' create a new treatment with the name 'cooling'. Next, create a segment in which the austenite domain will be cooled from 1300°C to 750°C with 1°C/s cooling rate
Kinetics simulation of simple cooling process
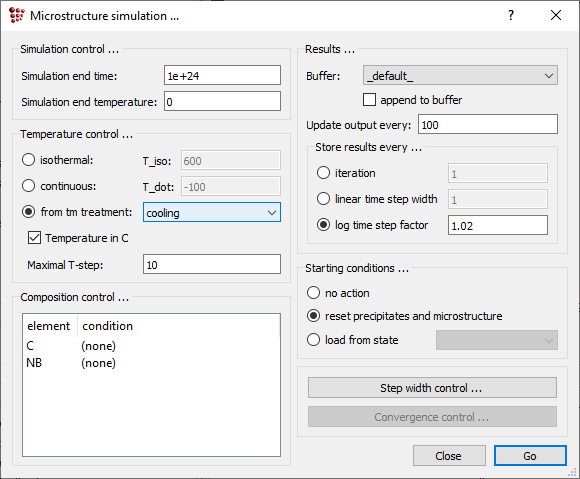
With all the setup procedures done, perform the kinetics simulation. Click on 'Calc' → 'Microstructure simulation'. Select the 'cooling' treatment in the 'Temperature control …' area and click on 'Go'.
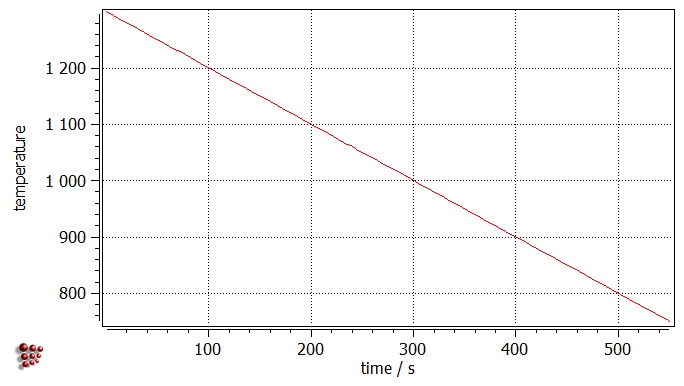
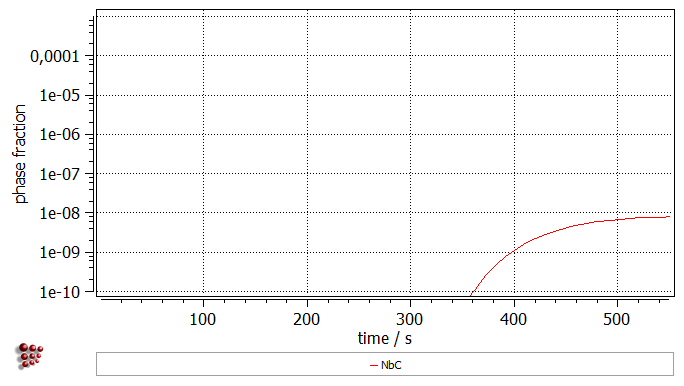
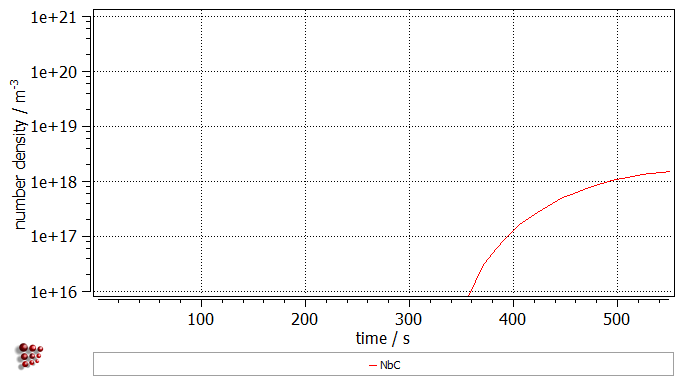
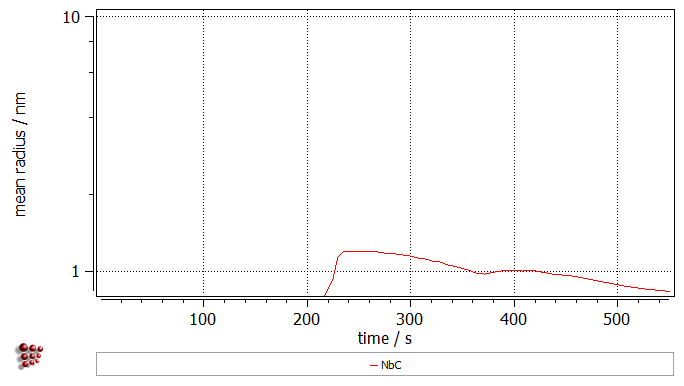
Once the calculation is completed, use the 'user defined plots' for visualizing the phase fraction, number density and mean radius evolution of the precipitates, as well as the temperature profile. Click on 'View' → 'Create new window', select the 'user-defined' tab and choose the entry '03_kinetics_4_frames_T_f_n_r_linX'. Click on 'OK'. Set the start of the scaling range to '1'. The analysis of the created plots reveals a somewhat unspectacular precipitaition of NbC phase after 200 s (below 1100°C) that reaches the number density of 1e18 m-3 and stays in the nanometer range.
By clicking on 'Global' → 'Buffers' → 'Rename', rename the current buffer to 'Cooling'.
Effect of volumetric misfit
In general, the precipitates show usually different crystallographic features from the matrix phase. This will be the source of the stress acting on the precipitates within the grain which needs to be considered especially during the nucleation stage. As for now, all the simulations were performed in the previous tutorial were neglecting this factor. Now it will be demonstrated how this effect can be intorduced into the simulation and what is the effect of it.
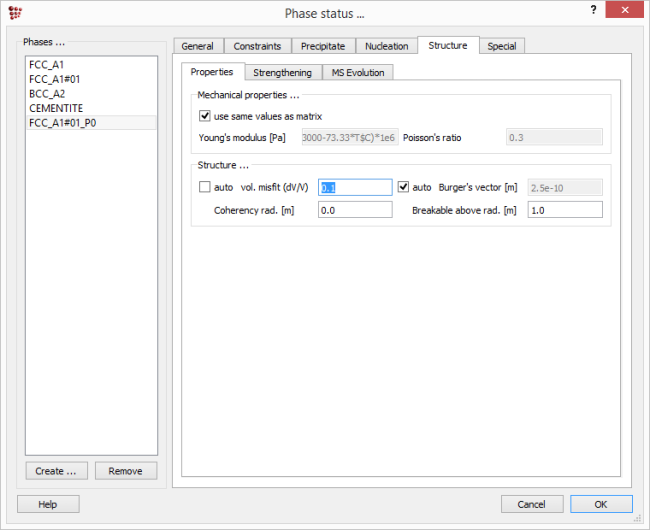
Click on 'Global' → 'Phase status' and select 'Structure' tab. In the field 'vol. misfit (dV/V)' type in the values of '0.1' for the precipitate phase. This represents the stress coming from the precipitate volume differing by 10% from the matrix volume.
Next, in 'Nucleation' → 'Controls' tab put a checkmark at the 'use volumetric misfit' for the precipitate phase.
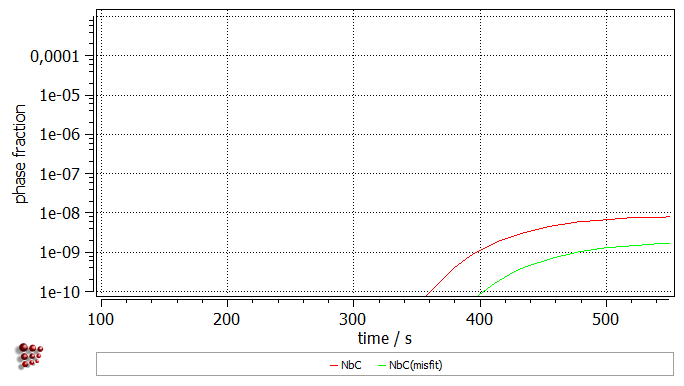
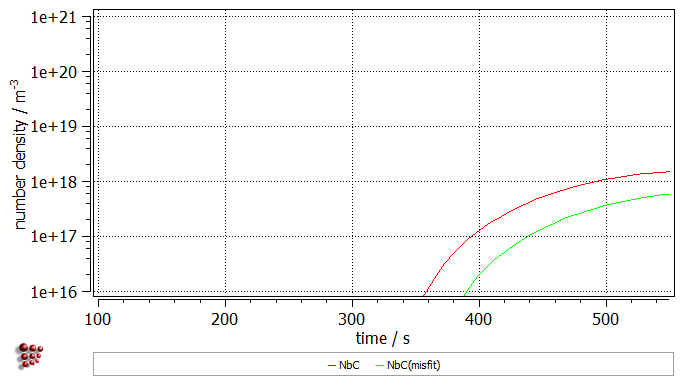
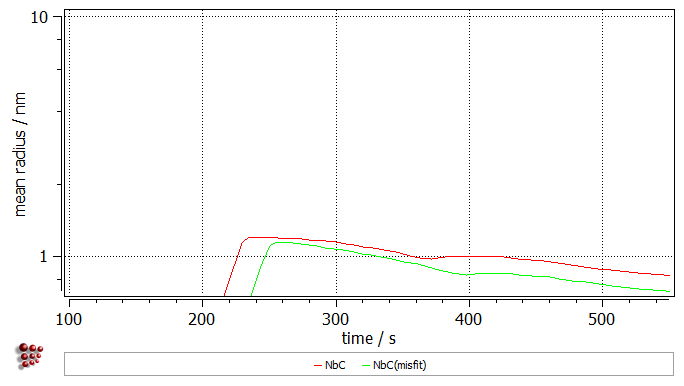
Click on 'OK' to close the window. Create a new buffer with the name 'Vol_misfit'. With this buffer selected, perform again the kinetic simulation. Once the simulation is completed, duplicate and lock all series in the plots, then switch the displayed buffer to 'Vol_misfit'. As it can be noticed, the definition of the volumetric misfit decreased amount of the precipitated phase.
Simulation of deformation process
When deformation process is to be simulated, there are basically three things to be modified in the treatment:
- Activation of the dislocation density evolution model.
- Definition of the deformation rates and temperatures.
- Deactivation of the volumetric misfit effect for the nucleation during the deformation.
Evolution of dislocation density
The deformation will change the microstructure of the alloy. Here, the change of the dislocation density by the deformation is presented.
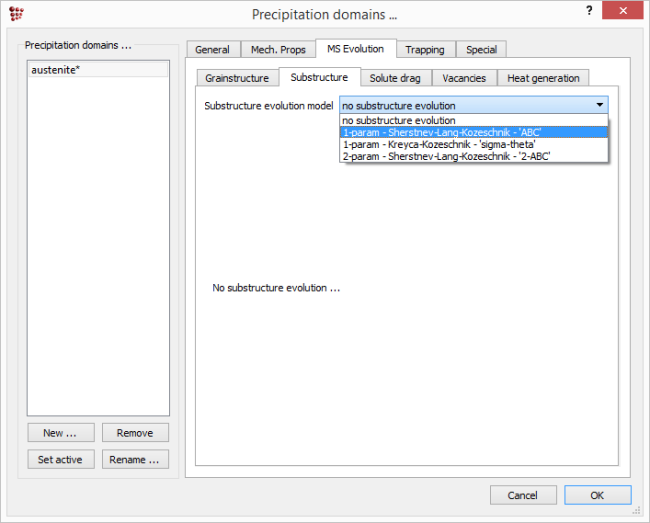
Click on 'Global' → 'Precipitation domains'. The simulated deformation will be performed in the austenite region, so select austenite as a precipitation domain and switch to the 'MS Evolution' tab. Inside, select 'Substructure' tab and select '1-param - Sherstnev-Lang-Kozeschnik - 'ABC'' as the model for the substructure evolution.
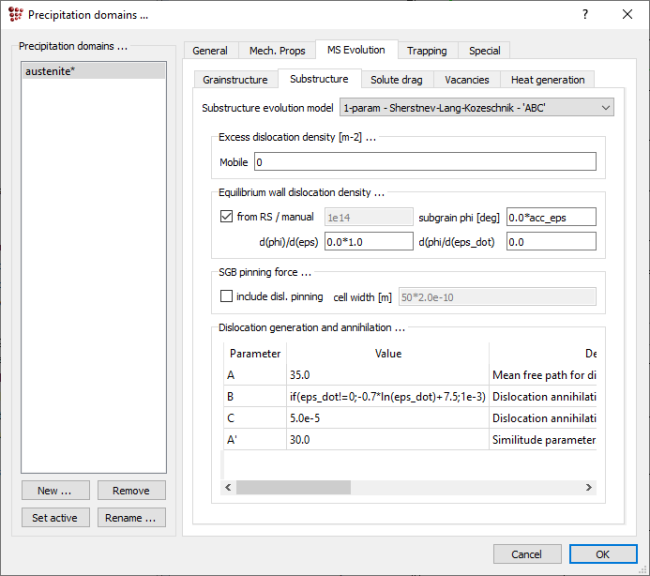
You might notice some parameters in the 'Dislocation generation and anihilation …' section which describe the generation of the dislocations ('A'-parameter) and their anihilation during the static ('B'-parameter, expressed as a conditional expression) and dynamic recovery ('C'-parameter). Leave all the parameters there on the default value.
Thermo-mechanical treatment settings
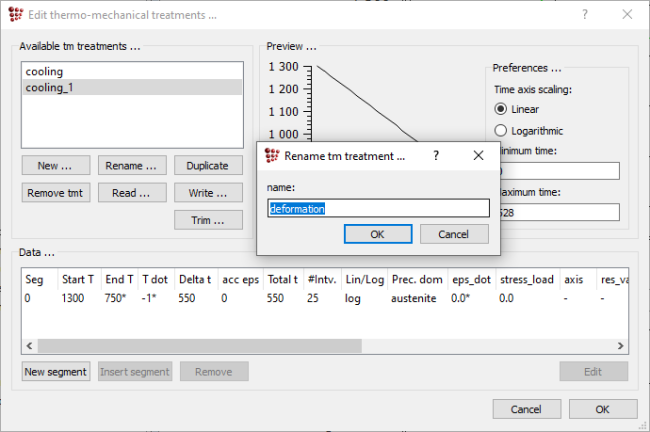
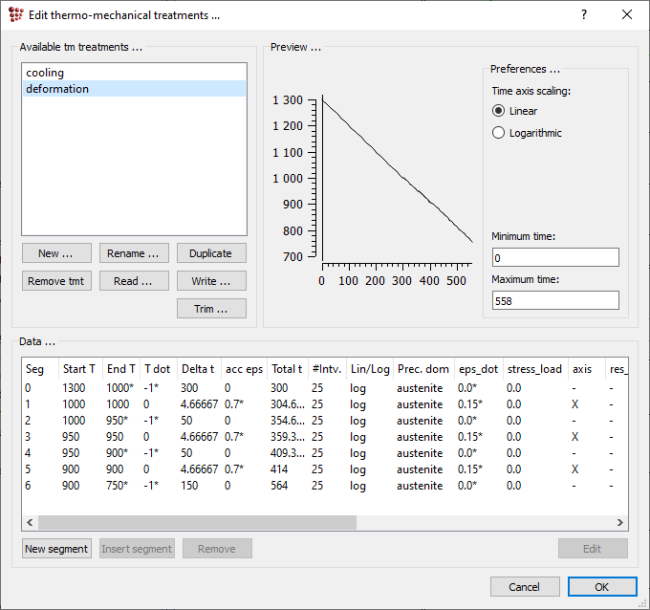
In this simulation, three deformation runs will be represented. Click on 'Global' → 'Thermo-mech. treatments', select 'cooling' treatment and click on 'Duplicate' button at the bottom of the list. A new treatment with name 'cooling_1' will be created. Select it and click on 'Rename' button. In the new window that appears, type 'deformation' as the new name and click on 'OK' button.
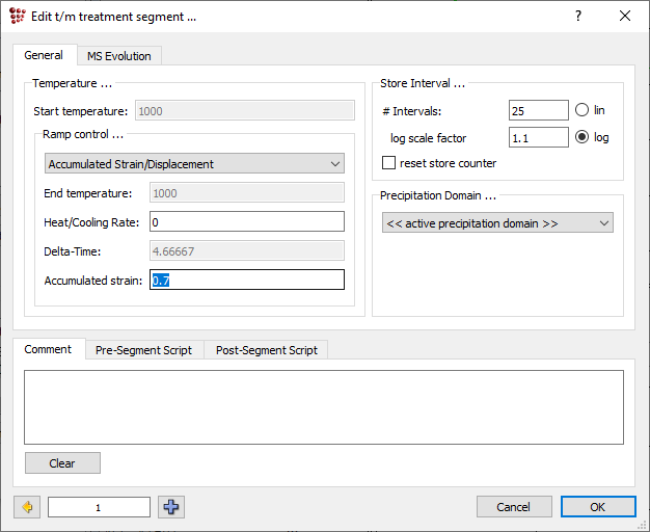
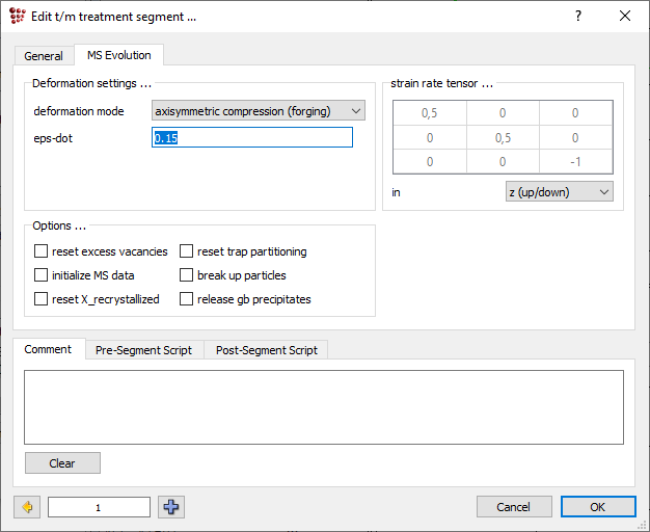
In the newly created treatment, modify the first segment end temperature to 1000°C. Add a new segment, change the ramp control setting therein to 'Accumulated strain' and set the 'Accumulated strain' value to '0.7'.
Afterwards, switch to the 'MS Evolution' tab and type in the strain_rate value of '0.15'.
The definition of the next segments should follow the settings below:
- End temperature of 950°C with 1 K/s rate.
- Deformation at 950°C with strain rate of 0.15 increasing the strain by 0.7.
- End temperature of 900°C with 1 K/s rate.
- Deformation at 900°C with strain rate of 0.15 increasing the strain by 0.7.
- End temperature of 750°C with 1 K/s rate.
The complete treatment data are shown below.
Deactivation of the volumetric misfit
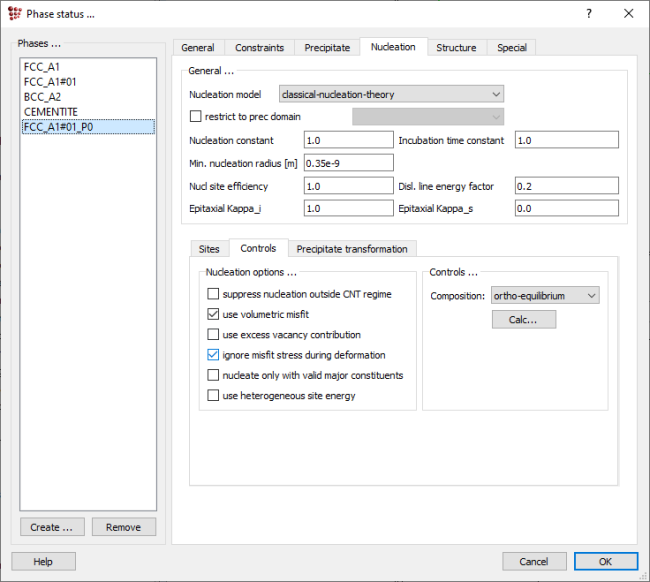
As previously mentioned, some volumetric misfit might be present related to the precipitates appearing in the grains, decreasing thus their nucleation rate. However, the stress introduced during the applied deformation can cancel this effect. To account for this in MatCalc, clicking on 'Global' → 'Phase status' and select the 'Nucleation' → 'Controls' tab. Put a checkmark at 'ignore misfit stress during deformation' for both precipitate phases. Click on 'OK' to close the window.
Kinetic simulation
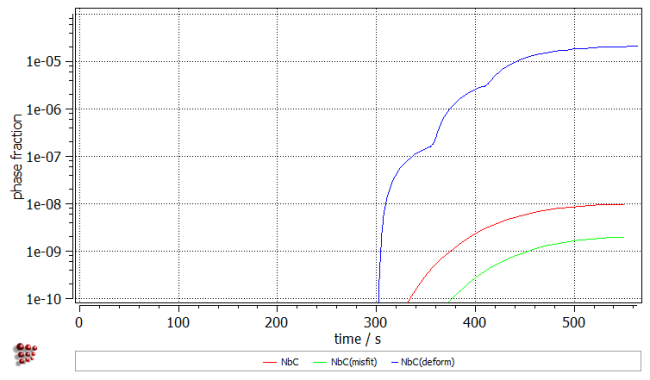
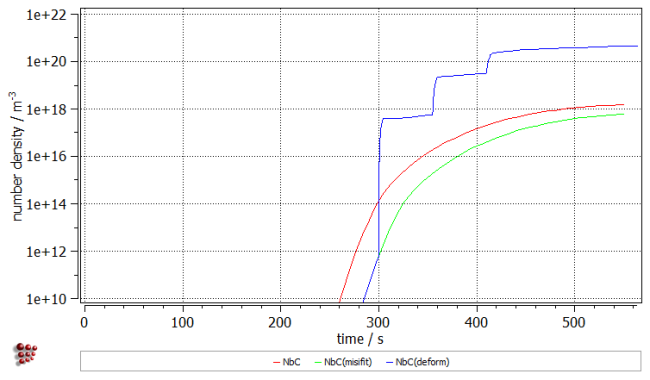
Click on 'Global' → 'Buffers' → 'Create' to create a new buffer with the name 'Deformation'. Afterwards, click on 'Calc' → 'Microstructure simulation' and select 'deformation' in 'from tm treatment:' field. Start the calculation by clicking on 'OK'. The results of the precipitation kinetics calculation are shown now with the blue curve.
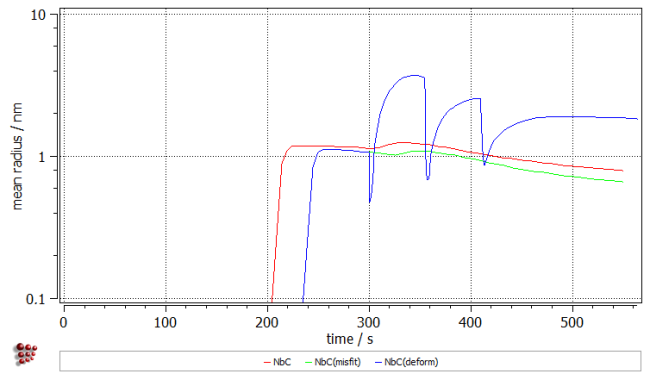
A considerable difference of three order of magnitudes is observed in the phase fraction of the precipitates. The same difference could be noticed for the number density. In both diagrams, three steps for the increase can be distinguished. The curve for the mean radius has a wavy form showing minima at the time frames of the sudden increases of the phase fraction and number density.
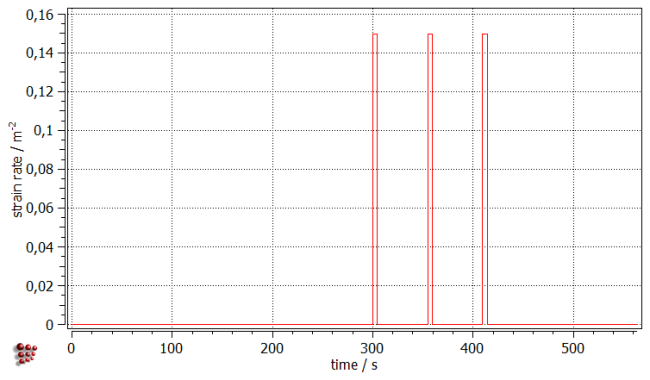
To have a closer inspection on the deformation influence on the precipitation kinetics, create a new plot window of 'p1'-type. Create three new plots, next to the existing one. Drag and drop the 'EPS_DOT' variable (located in 'kinetics: general' group), representing the strain rate in the system, onto the first plot. Three peaks can be recognized relevant for the three isothermal deformation segments.
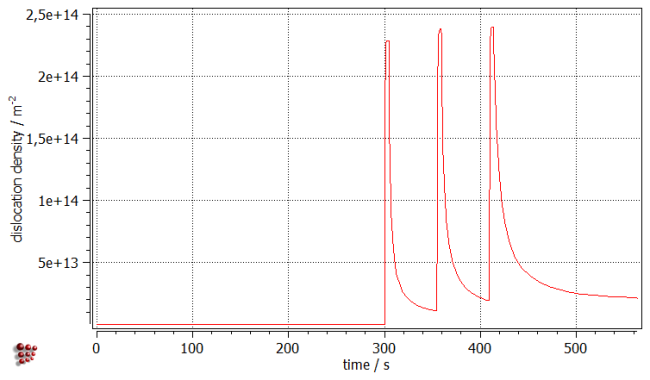
On the second diagramm, plot the 'DD_TOT$austenite' variable (located in 'prec_domain struct sc' group) representing the dislocation density of the system. Again, three peaks can be recognized with the maxima corresponding to those of strain rate curve on the first plot. Clearly, the material deformation increases the dislocation density. On the other hand, the dislocation density decreases during the segments without deformation - this is the time when static recovery occurs in the material.
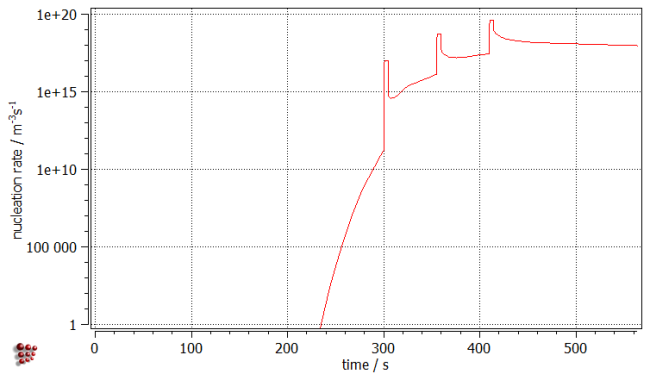
As dislocations were set as the nucleation sites for the precipitates, one might wonder if the increase in dislocation density has any effect on the precipitate nucleation. Drag and drop 'NUCL_RATE$FCC_A1#01_P0' variable (located in 'kinetics: nucleation' group), representing the nucleation rate of the precipitate phase, onto the third plot. Indeed, three peaks in nucleation rate series, corresponding to periods of increased dislocation density, can be recognized. Hence, one of the deformation effects on the precipitation process ia the acceleration of the nucleation kinetics by increasing the number of sites where the precipitate nuclei can form.
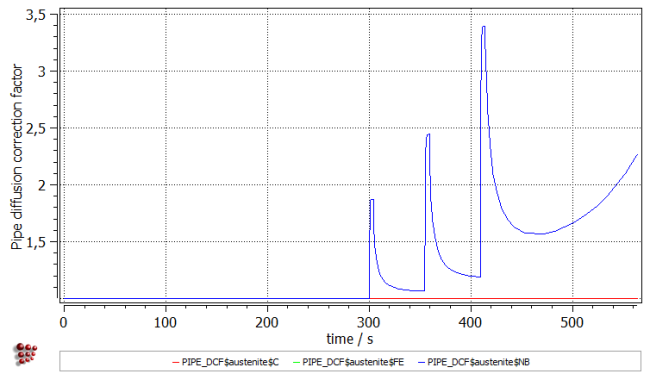
Another effect can be recognized, once 'PIPE_DCF$austenite$*' variables (located in 'prec_domain special' group) are plotted on the last diagramm. In order to explain the meaning of this variable, recall the pipe diffusion effect which is an effect of the enhanced diffusion along dislocations and is relevant for the precipitates nucleating there. In the simulations without any deformation, the pipe diffusivities are derived form the bulk diffusivities by multiplication of the latter with a factor dependent on the temperature. When dislocation density increases, an additional correction factor appears, which is dependent on the amount of the excess dislocations. The 'PIPE_DCF$austenite$*' variables represent this additional correction factor.
It can be noticed that for the segment before the deformation the factor has value of unity, as excess dislocations were not present in the system. Afterwards, three peaks can be observed again in accordance with the dislocation density peaks. This enhanced diffusion serves as an explanation for the higher precipitate mean radius which can be observed after the deformation segments.