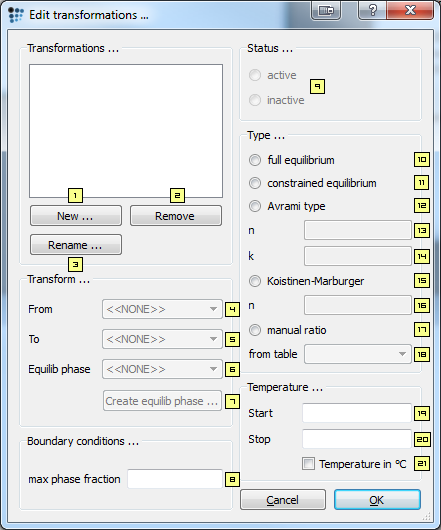
Transformations
The transformation dialog can be used to create 'solid transformations'. These represent recipes for how one phase in a MatCalc simulation ought to be transformed into another one. Typical application of transformations are the transformation of delta-ferrite into austenite in the Scheil simulation of peritectic reactions in steel (see, e.g., example E20-3 - Accounting for the peritectic reaction), or the transformation of one matrix phase into another one when evaluating the heat capacity of systems during DSC experiments.
A transformation is typically applied to phases which have dormant phase status. The transformation can occur according to different strategies
- The standard full equilibrium or constrained (para-) equilibrium condition is used to determine the phase fractions as a result of an equilibrium simulation. This is the common selection when using transformations in Scheil-Gulliver simulations.
- Alternatively, the transformation can be performed according to an Avrami equation with parameters $n$ and $k$. The transformed fraction $f$ is evaluated from the equation
\[ f = 1-exp(-kx^n) \]
The limits of the transformation are defined by the transformation start and end temperature. - For martensitic transformations, the Koistinen-Marburger equation can be used also. The transformation is then evaluated from
\[ f=1-exp(-n(M_s-T))\]
The limits of the transformation are given by the transformation start temperature, which is interpreted as the martensite start temperature $M_s$. The end temperature is not used in the Koistinen-Marburger equation. - For highest flexibility, the transformation progress can also be defined in terms of a table, where the phase fraction of the product phase is given in terms of X/Y pairs between the limits of the transformation start and end temperature.
Below, the dialog options are described in more detail.
- Create new transformation: Create a new transformation object.
- Remove: remove existing transformation.
- Rename: rename existing transformation.
- Transform From: A transformation always involves one phase which will be transformed into another. This selection defines the parent phase.
- Transform To: Product phase, into which the parent phase will be transformed.
- Transformation equilibrium phase: When using the transformation options full equilibrium and constrained equilibrium, an equilibrium phase must be created that is used to evaluate the transformed fraction. This phase can be created automatically by using the Create transformation equilibrium phase button.
- Create transformation equilibrium phase: Creates a transformation phase with the suffix '_T' and a transformation solid phase with the suffix '_TS'.
- Maximum phase fraction: Usually, the transformation converts the entire parent phase into a product phase. With this setting, the total transformed fraction can be limited to a smaller value.
- Status: When selecting 'active', the transformation will be applied in the next simulation.
- Full equilibrium: The full, unconstrained equilibrium simulation will be used to evaluate the transformed fraction.
- Constrained equilibrium: Para-equilibrium will be used to evaluate the transformed fraction.
- Avrami type: Selection of this option activates the Avrami equation for controlling the transformation progress.
- n-factor for Avrami type: $n$ value in Avrami equation.
- k-factor for Avrami type: $k$ value in Avrami equation.
- Koistinen-Marburger type: Selection of this option activates the Koistinen-Marburger equation for controlling the transformation progress.
- n-factor for Koistinen-Marburger type: $n$ value in Avrami equation.
- Manual ratio: Use a table to control the transformation progress.
- data from table: Corresponding table name.
- Start temperature: Apply transformation only below the start temperature.
- Stop temperature: Finish transformation at the stop temperature.
- Temperature in Celsius: C ↔ K.