Table of Contents
Example MP10: Yield strength prediction in Ni-base superalloy with shearable γ' and γ'' precipitates
Compatibility
MatCalc version: 5.53.0027
Database: mc_ni.tdb, mc_sample_ni.ddb
Author: M.R. Ahmadi
Created: 2013-12-06
Revisions:
Objectives
A sample heat treatment of the Inconel-718 alloy is shown. The material yield strength is evaluated. The contributions of various material properties to the yield strength are also discussed.
Complementary files
Click here to view the script for this tutorial.
Main document
Setup thermodynamics
Set up the thermodynamics by loading the mc_ni database
Select the following phases, elements and enter the chemical composition in wt-%:
| Elements | Chemical composition [wt.%] | Phases |
|---|---|---|
| Al | 1.5 | FCC_A1 |
| C | 0.03 | DELTA |
| Co | 9.1 | GAMMA_PRIME |
| Cr | 17.4 | GAMMA_DP |
| Fe | 9.7 | |
| Mo | 2.7 | |
| Nb | 5.5 | |
| Ti | 0.7 | |
| W | 1.0 |
Set Ni to reference element. Continue in the thermodynamic setup by loading the diffusion database for Ni (mc_sample_ni.ddb). To ensure correct thermodynamic values and no driving force errors (DFM-errors), set automatic start values and calculate an equilibrium at 1000°C.
Precipitation domain and precipitates
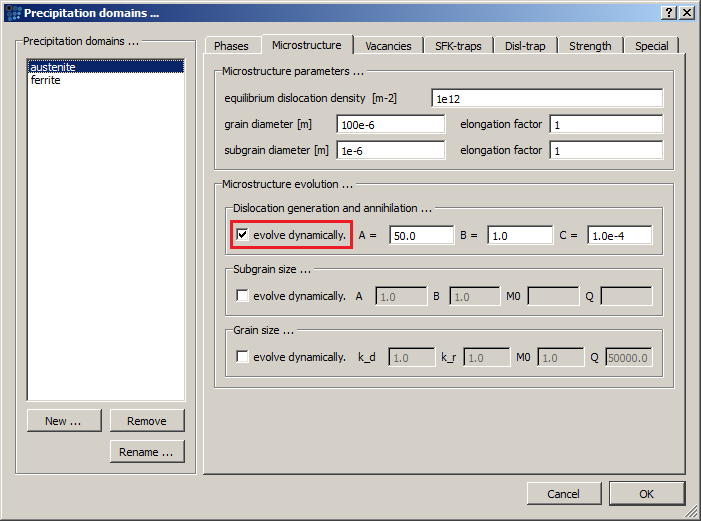
Create a precipitation domain with the name 'nickel_matrix' with FCC_A1 matrix phase. Change the value of Taylor factor to 2.6. Leave all other domain settings on default value.
Follow by setting up the precipitates. Create one precipitate phase for gamma_prime phase and one for the delta phase. Choose the settings of the precipitate phases, as given in the table below
| Precipitate | Tab | Option | Value |
|---|---|---|---|
| cementite_p0 | Precipitate | #size classes | 25 (Initialize!) |
| cementite_p0 | Attached to pd | ferrite | |
| cementite_p0 | Kinetic alias name | Cementite | |
| cementite_p0 | Nucl. sites | Nucleation sites | dislocations |
| Precipitate | Tab | Option | Value |
|---|---|---|---|
| fcc_a1#01_p0 | Precipitate | #size classes | 25 (Initialize!) |
| fcc_a1#01_p0 | Kinetic alias name | NbC(aust,d) | |
| fcc_a1#01_p0 | Nucleation | Restrict nucleation to prec domain | ✔, select austenite |
| fcc_a1#01_p0 | Nucl. sites | Nucleation sites | dislocations |
| Precipitate | Tab | Option | Value |
|---|---|---|---|
| fcc_a1#01_p1 | Precipitate | #size classes | 25 (Initialize!) |
| fcc_a1#01_p1 | Kinetic alias name | NbC(aust,gb) | |
| fcc_a1#01_p1 | Nucleation | Restrict nucleation to prec domain | ✔, select ferrite |
| fcc_a1#01_p1 | Nucl. sites | Nucleation sites | grain boundary |
| Precipitate | Tab | Option | Value |
|---|---|---|---|
| AlN_p0 | Precipitate | #size classes | 25 (Initialize!) |
| AlN_p0 | Kinetic alias name | AlN(aust,d) | |
| AlN_p0 | Nucleation | Restrict nucleation to prec domain | ✔, select austenite |
| AlN_p0 | Account for coherent misfit stress | ✔ | |
| AlN_p0 | Nucl. sites | Nucleation sites | dislocations |
| AlN_p0 | Structure | Vol. misfit | 0.27, remove ✔ from 'auto' |
| Precipitate | Tab | Option | Value |
|---|---|---|---|
| AlN_p1 | Precipitate | #size classes | 25 (Initialize!) |
| AlN_p1 | Kinetic alias name | AlN(aust,gb) | |
| AlN_p1 | Nucleation | Restrict nucleation to prec domain | ✔, select austenite |
| AlN_p1 | Nucl. sites | Nucleation sites | grain boundary |
| Precipitate | Tab | Option | Value |
|---|---|---|---|
| AlN_p2 | Precipitate | #size classes | 25 (Initialize!) |
| AlN_p2 | Kinetic alias name | AlN(ferr,d) | |
| AlN_p2 | Nucleation | Restrict nucleation to prec domain | ✔, select ferrite |
| AlN_p2 | Account for coherent misfit stress | ✔ | |
| AlN_p2 | Nucl. sites | Nucleation sites | dislocations |
| AlN_p2 | Structure | Vol. misfit | 0.27, remove ✔ from 'auto' |
| Precipitate | Tab | Option | Value |
|---|---|---|---|
| AlN_p3 | Precipitate | #size classes | 25 (Initialize!) |
| AlN_p3 | Kinetic alias name | AlN(ferr,gb) | |
| AlN_p3 | Nucleation | Restrict nucleation to prec domain | ✔, select ferrite |
| AlN_p3 | Nucl. sites | Nucleation sites | grain boundary |
Heat treatment
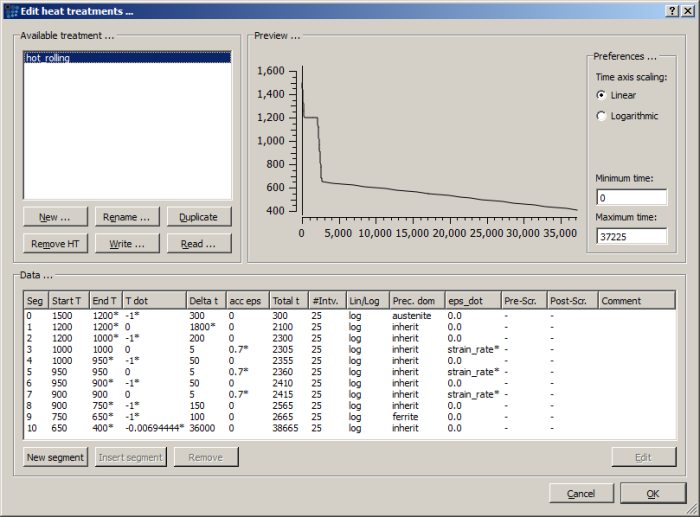
Define the heat treatment with the following segments:
- Start at temperature of 1500 C. Cool down to 1200 C with 1 C/s cooling rate. Select austenite as precipitation domain.
- Hold at 1200 C for 30 minutes.
- Cool down to 1000 C with 1 C/s cooling rate.
- Cool down to 950 C with 1 C/s cooling rate.
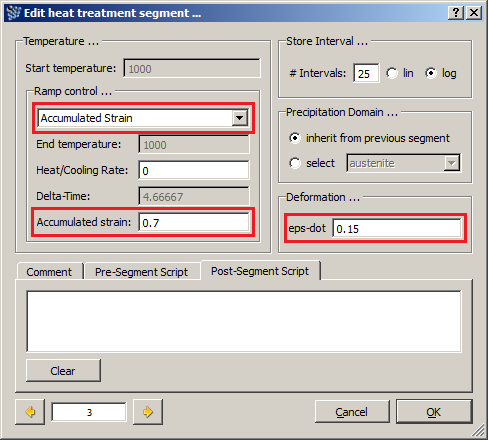
- Deform material with the strain rate of 0.15 till the accumulated strain reaches the 0.7 value. Hold the material at 950 C (cooling rate is 0 C/s).
- Cool down to 900 C with 1 C/s cooling rate.
- Deform material with the strain rate of 0.15 till the accumulated strain reaches the 0.7 value. Hold the material at 900 C (cooling rate is 0 C/s).
- Cool down to 750 C with 1 C/s cooling rate.
- Cool down to 650 C with 1 C/s cooling rate. Switch precipitation domain to ferrite.
- Cool down to 400 C within 10 hours.
Precipitation simulation
Before starting the simulation, create 4 diagrams which will describe the precipitation characteristics (temperature, phase fraction, number densities, mean radii) - this is conveniently done by clicking on 'View' → 'Create new window …' → 'user-defined' tab → '03_kinetics_4_frames_T_f_n_r_linX'. Start the simulation with the temperature controlled by the defined heat-treatment.
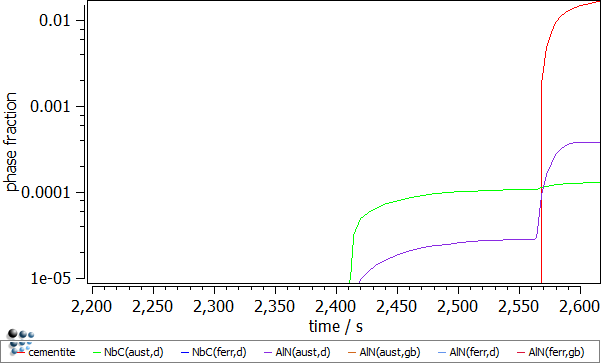
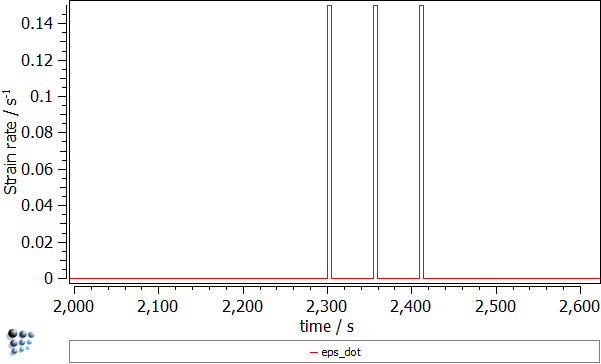
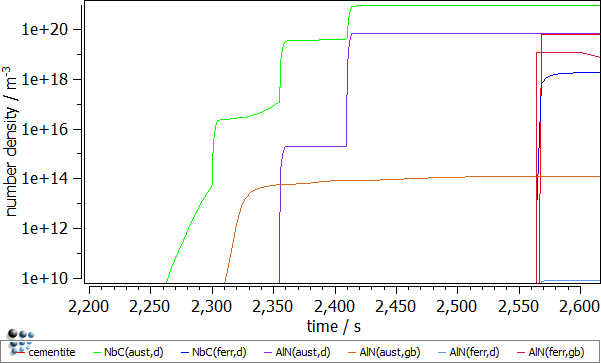
The first look on the calculation results suggests that the whole precipitation appears in the ferrite domain (after ~2560 seconds). By magnifying the time axis (default x-axis!) from 2200 to 2600 seconds, one can notice the precipitates occurring in the austenite domain already where the deformation stage was introduced.
This deformation process can be illustrated by the following plots:
- Strain rate ('EPS_DOT' variable found in the 'kinetics:general' group). The three peaks correspond to the deformation segments.
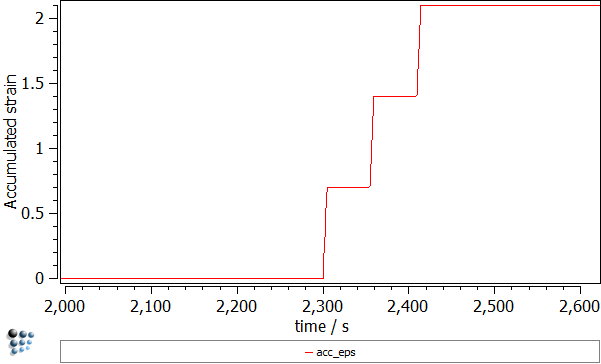
- Strain accumulated in the sample ('ACC_EPS' variable found in the 'kinetics:general' group). Every deformation segment resulted in increasing the strain by 0.7.
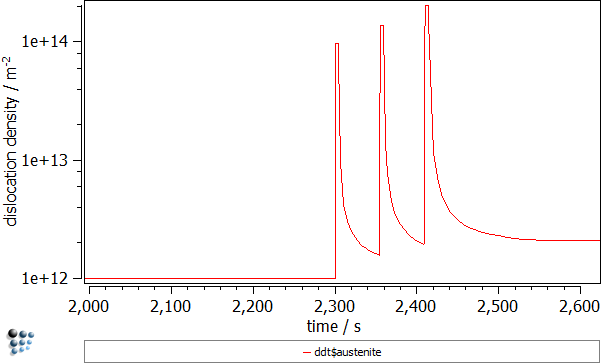
- Dislocation density in the austenite ('DDT$austenite' variable found in the 'kinetics:pd struct' group). Again, three peaks corresponding to the deformation stages can be recognized. The dislocation density rises by two orders of magnitude.
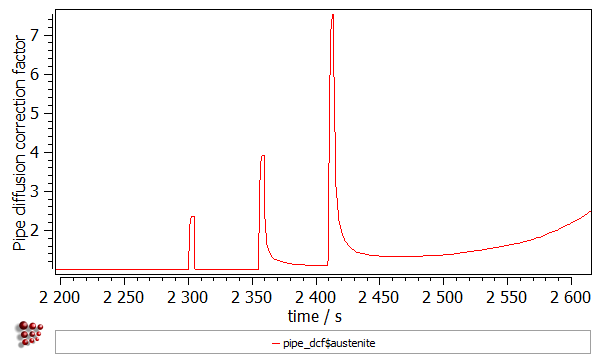
- Pipe diffusion correction factor ('PIPE_DCF$austenite$*' variable found in the 'kinetics:pd special' group). The dislocations allow for a faster diffusion of the atoms. This effect is known as “pipe diffusion” and is represented with a correction factor, by which the diffusion coefficients of elements are multiplied (the same factor is assumed for all elements). The magnitude of this factor depends on the amount of the excess dislocation density and temperature. Increasing the number of dislocations during the deformation results in the faster diffusion in the material.
The influence of the deformation on the precipitation kinetics can be discussed on the following two plots:
- Number density of the precipitates. The number of precipitates nucleating on dislocations in austenite is increasing significantly during the deformation segments. Three increments for NbC(aust,d) and two for AlN(aust,d) precipitates can be identified. This observation is explained by the increasing number of the dislocations and thus the increasing number of the available nucleation sites for those precipitates.
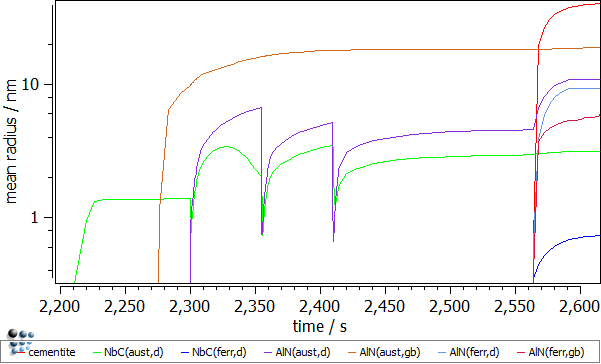
- Mean radii of the precipitates. The rapid descent of the mean radius for the NbC(aust,d) and AlN(aust,d) precipitates nucleating at dislocations is observed during the dislocation segments. This is an effect of the outburst of the new nuclei for these phases. These falls are immediately compensated by the significant radius growth which is a result of the enhanced diffusion due to the increased dislocation number (pipe-diffusion).
Comparison with no deformation case
In order to demonstrate the effects of the deformation on the precipitation process, the calculation will be repeated for the system without any deformation steps. Rename the current buffer to 'w_deform'. Create the new buffer and rename it to 'no_deform'. Duplicate and lock all series in the plots. Next, edit the segments which describe the deformation stages in the heat treatment and write zero to 'eps-dot'. In options window for the plots switch the displayed buffer to 'no_deform' and start the precipitation kinetics calculation.
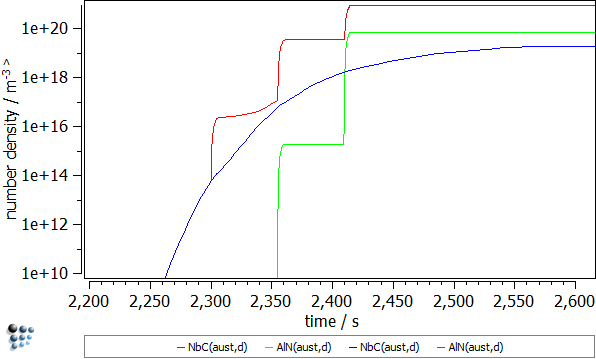
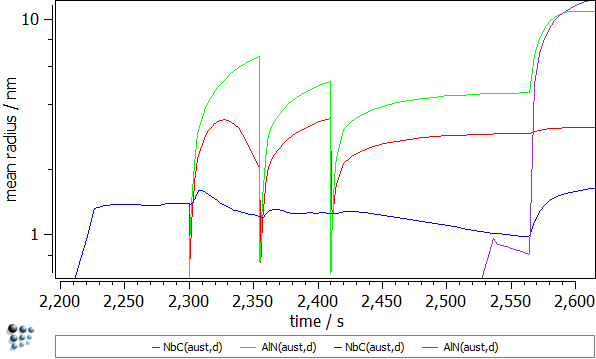
Let's compare the results for the NbC(aust,d) and AlN(aust,d) from the both simulations
- Number densities. The number densities for these phases are a few order smaller than in the deformed material. The phase fractions show a similar behavior. Noteworthy, the precipitates for AlN are virtually non-existent in the samples without strain. As expected, the excess dislocations increase the nucleation rates in the deformed material resulting in the higher number of precipitates.
- Mean radii. The differences here are not very prominent. Nevertheless, the radii in the strained samples are larger, as the introduced dislocations enable the pipe-diffusion.