MatCalc version: 5.52.0038
Database: mc_sample_fe.tdb
Author: P. Warczok
Created: 2013-06-25
Revisions:

This example investigates the most likely nucleus composition of the homogeneous precipitate phase. The analysis is based on the classical nucleation theory predicition of the critical nucleation Gibbs energy which is given as:

This energy depends strongly (cosider the exponents!) on two parameters: which stands for the driving force of the precipitate formation expressed per volume and which stands for the precipitate-matrix interfacial energy. Both of these parameters are evaluated from the thermodynamic data provided with the database.

In this example, a binary system with 1.5 at.% Cu at 500°C will be studied. As it will be shown, at this conditions a homogeneous precipitate phase is expected to form. An analysis of the thermodynamic driving force for the formation of this phase combined with the evaluation of the energy of the newly created interface between the two phases will reveal the critical nucleation Gibbs energy. A composition of the new phase at which the Gibbs energy will have a minimal value is expected to be identical with the first nucleus composition.

This example follows the analysis presented in ref.¹⁾.

• E6 - Composition-dependent driving forces for carbide precipitation in Fe-C-Cr - The evaluation of the driving force for the precipitate formation is needed for reaching the objective of the current example. Therefore, the user is recommended to become acquainted with the content of example E6.
• Evaluation of interfacial energies - A technical paper which describes how the value of the interfacial energy is obtained.

Click here to view the script for this example.

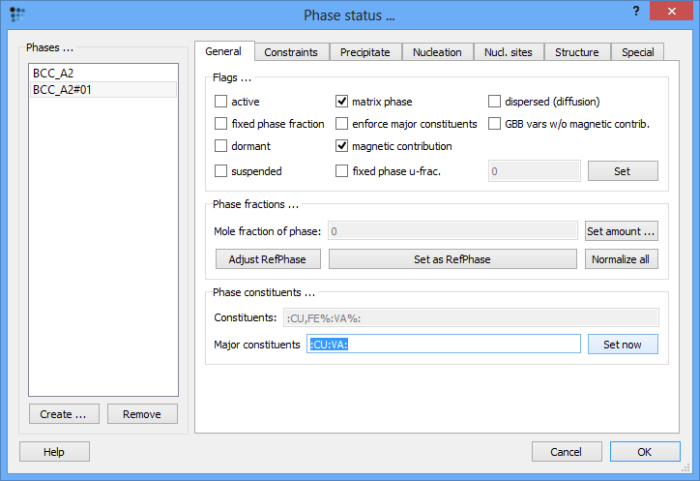
In the new workspace, open one of the above listed databases and select the elements Fe and Cu, as well as the phase BCC_A2. Set a chemical composition of 3 at.% Cu.
The studied system should consist of two phases: the supersaturated solid solution and the precipitate phase which is to form. In this example, both of those have the same a body centered cubic structure. However, after reading the thermodynamic database, only one phase is present. Thus, create a second equilibrium 'BCC_A2' phase. As this should be the Cu-rich phase, replace Fe with Cu as its major constituent.

Set automatic start values and calculate an equilibrium at 500°C. The result obtained in 'Phase details' window should appear like this (while the exact numbers might differ depending on the thermodynamic database used, the magnitude of the values should be the same):

#### /BCC_A2/ moles: 0,97111, gm: -28406.9 (-28406.9), sff: 1
Phasestatus: entered - active
FE +9.98780e-001  CU +1.22033e-003  

#### /BCC_A2#01/ moles: 0,0288895, gm: -29295.7 (-29295.7), sff: 1
Phasestatus: entered - active
CU +9.97417e-001  FE +2.58303e-003  

### inactive ###

This result informs that the system reaches the minimal value of the Gibbs energy when it consists of two phases which are almost pure Fe and pure Cu. Considering the phase fractions, it can be concluded that an experimental picture would show some copper precipitates present in the iron matrix. This thermodynamical analysis does not include the energy contribution of the newly created interfaces between the two phases, though. Indeed, this contribution might be neglected for the system with few big precipitates, when the total interface area is small. However, it must be still considered at the nucleation stage, when the interface of many small nuclei sum up to a considerable area.

The paraequilibrium stepped calculation will allow to study the parameter values for the system when the composition of a given phase is changed, rather than the composition of the whole system. This kind of calculation will allow to study the dependence of the interfacial energy and the driving force for formation of the precipitate phase depending on its composition.
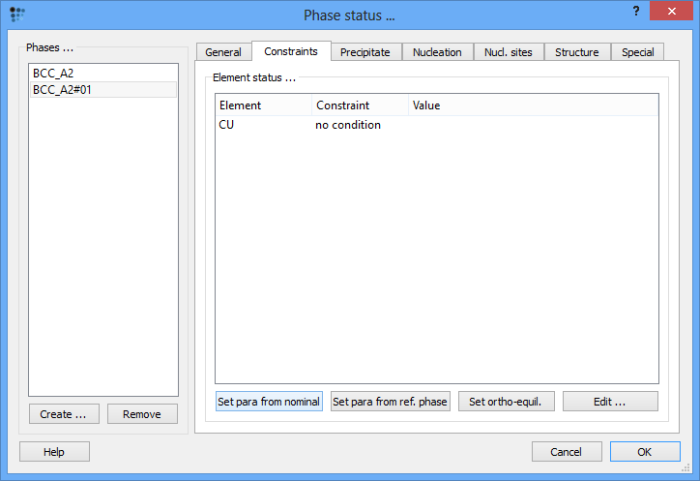
In the 'Phase details' window, select the 'BCC_A2#01' phase, switch to the 'Constraints' tab and click on the 'Set para from nominal' button. This will set a u-fraction of Cu equal to the global composition.

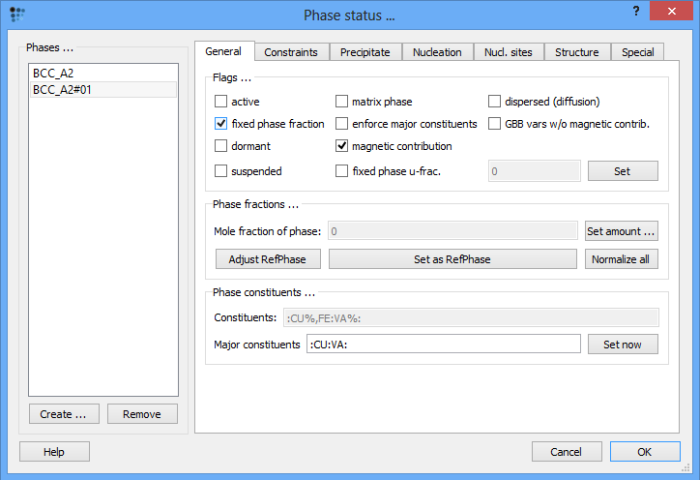
In the 'General' tab, set the phase fraction of this phase to zero and check the 'fixed phase fraction' box. This step ensures that the driving force for the phase formation is evaluated though the phase itself is absent in the system.

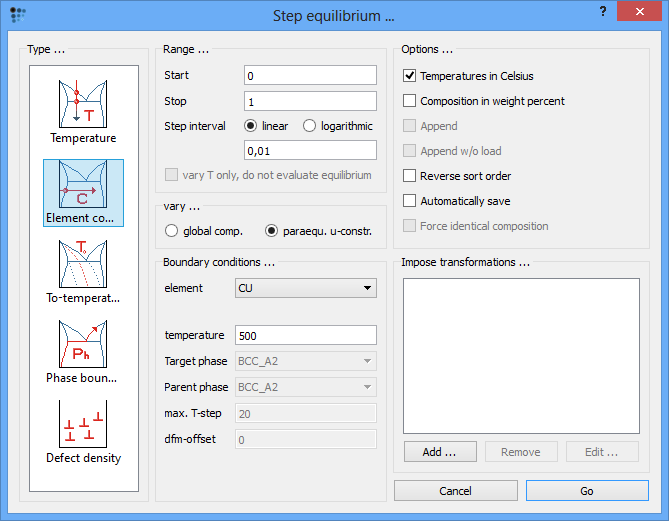
Calculate an equilibrium once again. Next, open the 'Step equilibrium' window and select the 'element con…' type of the calculation. Set the range over the whole composition with 0.01 step. Ensure that the temperature is set to 500°C and the 'Composition in weight percent' box is unchecked. Clearly, an important point is to select 'paraequ. u-constr.' in the 'vary…' field instead of the default 'global comp.'.

Click on 'Go'

When the calculation is ready, create a new plot window (p1). The following plots will be of interest:

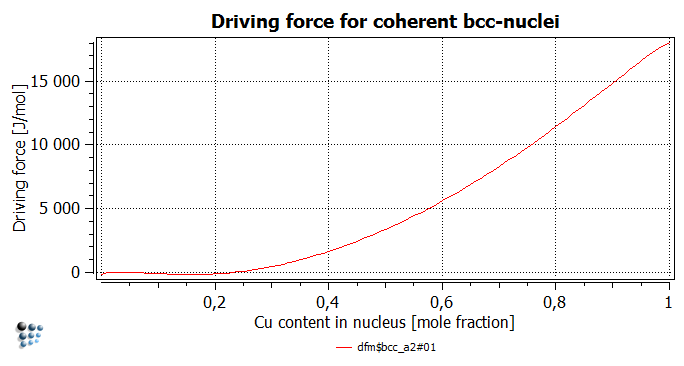
- Driving force for the formation of the precipitate phase
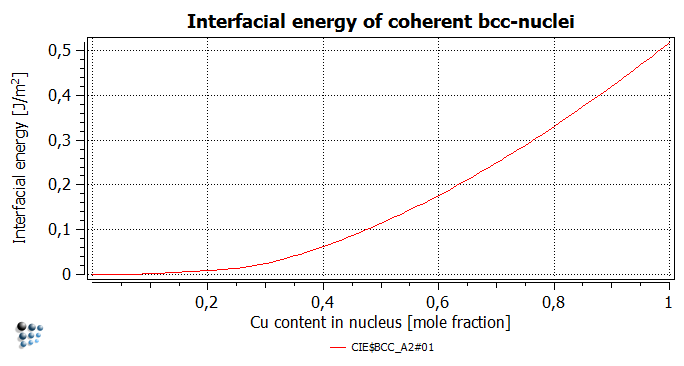
- Interfacial energy for the precipitate phase

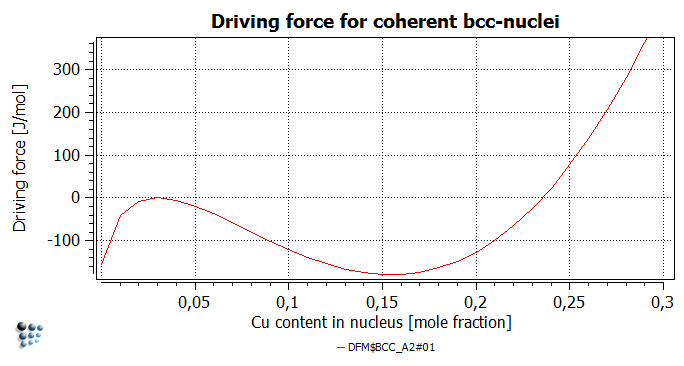
The driving force for the Cu-rich phase formation ('DFM$BCC_A2#01' variable found in 'driving forces' group) has non-positive values for Cu contents below 24 at.%. This indicates that the creation of any coherent nuclei with the Cu content below this value is not expected to happen, as it would increase the Gibbs energy of the system.

The interfacial energy of the Cu-rich nuclei ('CIE$BCC_A2#01' variable found in 'state variables GBB' group) is increasing monotonically with the Cu content of the nuclei. This is due to the fact that the more copper in the precipitate, the more energy-rich Fe-Cu bonds at the interface are present. Further details on the evaluation of the interfacial energy are given in this technical paper

In order to calculate the critical nucleation Gibbs energy, define a function according to the equation cited in the introduction to this example. One needs to keep in mind, that the driving forces present in the equation defining the critical nucleation Gibbs energy are expressed per volume (m³) instead of amount (mol). Hence, the driving forces are to be divided by the molar volume of the system. This parameter is represented in MatCalc by 'VM' variable found in 'mass/volume/density' group. The syntax for the function (named in the script as 'cnge') should look like this:

(16*pi*(cie$bcc_a2#01)^3)/(3*(dfm$bcc_a2#01/vm)^2)

Important note …

* MatCalc has a built-in variable 'PI' which has a value corresponding to the mathematical constant

* Unless a physical database is loaded, variable 'VM' has a default value of 7e-6 m³mol^-1.

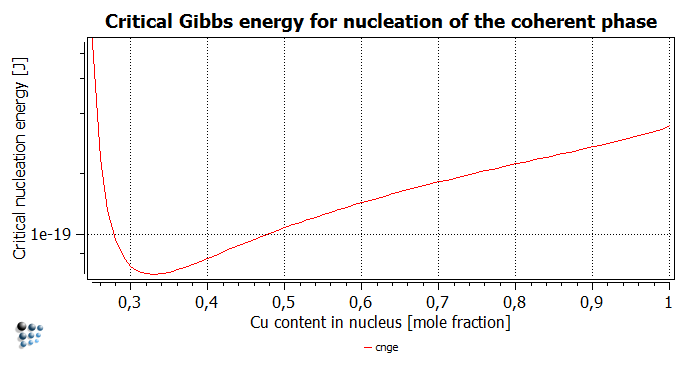
The plot of the function for the whole composition range looks a little strange for the first moment - A curve with two sharp extrema (use a logarithmic scaling for y-axis!). The extrema correspond to the compositions for which the driving force equals zero, in which case the critical energy goes to infinity. However, the values for the composition range below 24 at.% Cu have no physical meaning, as this is the range where the driving force is negative and the precipitate will not form, anyway. An investigation of the compostion range above 25 at.% of Cu will reveal a minimum of the critical nucleation Gibbs energy for the nuclei consisting of ~33 at.% of Cu with the value of ~6,29*10^-20 joules per nucleus. But does it mean that nuclei with this composition will be the only one to form? Before this question is answered, store this minimal Gibbs energy value as a variable 'cnge_min'.

The critical nucleation Gibbs energy can be used as an input parameter for the statistical analysis. The probability of the nucleation of an embryo with a specific composition is dependent on its critical nucleation Gibbs energy as:

\[ P(x_{Cu}) \approx exp \LARGE(\normalsize - \frac{G^{*}(x_{Cu})}{k_{B}T}\LARGE) \]

with being the Boltzmann constant. While calculation of the exact probability values might be a laborious task (due to the evaluation of the normalization constant), an estimation of the values relative to the maximal probability is rather straightforward. The scaled probability is thus defined as:

\[ P_{rel}(x_{Cu}) = \frac{P(x_{Cu})}{P_{max}} = exp\LARGE(\normalsize \frac{G^{*}_{min}-G^{*}(x_{Cu})}{k_{B}T}\LARGE) \]

Define a new function 'rel_prob' as:

 exp((cnge_min-cnge)*na/r/t)

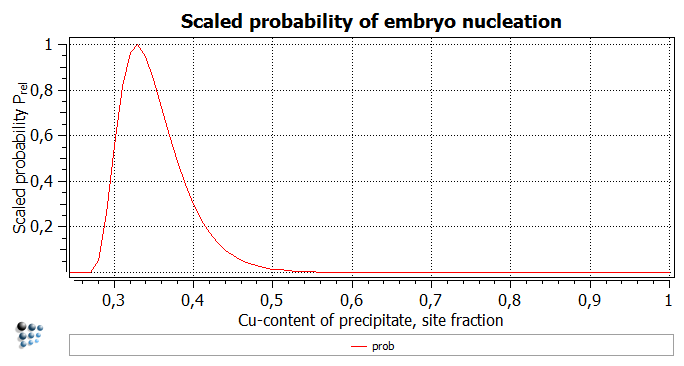
Next, plot this function. This diagram shows the relative frequency of the embryo nucleation depending on its composition. The reference is set to the most frequent appearing nucleus with 33 at.% Cu. Still the nucleated embryos need not to have strict this composition. One can find half as much embryos containing 38 at.% Cu as the ones with 33 at.%, for instance. The occurence of the nuclei consisting of more than 50 at.% Cu will be a very rare event (relative probability is lower than 0.01). The thermodynamic calculation showed that in the equilibrated system, the content of the Cu-rich phase is ~99.7 at.%. Remarkably, an embryo with this composition will appear every 10^-11 times the one with the lowest nucleation energy - one needs a logarithmic scale to find this value at all. It is interesting to note that the Cu-rich phase does not seem to nucleate with the Cu-rich embryos…

none